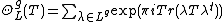“Siegel theta series”的意思、由来-开放百科全书

词条

Siegel theta series

释义

Definition
References

In mathematics, a Siegel theta series is a Siegel modular form associated to a positive definite lattice, generalizing the 1-variable theta function of a lattice.

Definition

Suppose that L is a positive definite lattice. The Siegel theta series of degree g is defined by

where T is an element of the Siegel upper half plane of degree g.

This is a Siegel modular form of degree d and weight dim(L)/2 for some subgroup of the Siegel modular group. If the lattice L is even and unimodular then this is a Siegel modular form for the full Siegel modular group.

When the degree is 1 this is just the usual theta function of a lattice.

References

{{citation|mr=0871067

|last=Freitag|first= E.
|title=Siegelsche Modulfunktionen
|series=Grundlehren der Mathematischen Wissenschaften |volume= 254. Springer-Verlag|place= Berlin|year= 1983|isbn= 3-540-11661-3 }}

1 : Automorphic forms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。