- Complete graphs
- Relation to degree
- Planar graphs
- Complexity
- Notes
- References
In graph drawing and geometric graph theory, the slope number of a graph is the minimum possible number of distinct slopes of edges in a drawing of the graph in which vertices are represented as points in the Euclidean plane and edges are represented as line segments that do not pass through any non-incident vertex.
Complete graphs
Although closely related problems in discrete geometry had been studied earlier, e.g. by {{harvtxt|Scott|1970}} and {{harvtxt|Jamison|1984}},
the problem of determining the slope number of a graph was introduced by {{harvtxt|Wade|Chu|1994}}, who showed that the slope number of an {{mvar|n}}-vertex complete graph {{math|Kn}} is exactly {{mvar|n}}. A drawing with this slope number may be formed by placing the vertices of the graph on a regular polygon.
Relation to degree
The slope number of a graph of maximum degree {{mvar|d}} is clearly at least 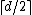 , because at most two of the incident edges at a degree-{{mvar|d}} vertex can share a slope. More precisely, the slope number is at least equal to the linear arboricity of the graph, since the edges of a single slope must form a linear forest, and the linear arboricity in turn is at least
, because at most two of the incident edges at a degree-{{mvar|d}} vertex can share a slope. More precisely, the slope number is at least equal to the linear arboricity of the graph, since the edges of a single slope must form a linear forest, and the linear arboricity in turn is at least 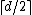 .
.
There exist graphs with maximum degree five that have arbitrarily large slope number.[1] However, every graph of maximum degree three has slope number at most four;[2] the result of {{harvtxt|Wade|Chu|1994}} for the complete graph {{math|K4}} shows that this is tight. Not every set of four slopes is suitable for drawing all degree-3 graphs: a set of slopes is suitable for this purpose if and only it forms the slopes of the sides and diagonals of a parallelogram. In particular, any degree 3 graph can be drawn so that its edges are either axis-parallel or parallel to the main diagonals of the integer lattice.[3] It is not known whether graphs of maximum degree four have bounded or unbounded slope number.[4]
Planar graphs
As {{harvtxt|Keszegh|Pach|Pálvölgyi|2011}} showed, every planar graph has a planar straight-line drawing in which the number of distinct slopes is a function of the degree of the graph. Their proof follows a construction of {{harvtxt|Malitz|Papakostas|1994}} for bounding the angular resolution of planar graphs as a function of degree, by completing the graph to a maximal planar graph without increasing its degree by more than a constant factor, and applying the circle packing theorem to represent this augmented graph as a collection of tangent circles. If the degree of the initial graph is bounded, the ratio between the radii of adjacent circles in the packing will also be bounded,[5] which in turn implies that using a quadtree to place each graph vertex on a point within its circle will produce slopes that are ratios of small integers. The number of distinct slopes produced by this construction is exponential in the degree of the graph.
Complexity
It is NP-complete to determine whether a graph has slope number two.[6] From this, it follows that it is NP-hard to determine the slope number of an arbitrary graph, or to approximate it with an approximation ratio better than 3/2.
It is also NP-complete to determine whether a planar graph has a planar drawing with slope number two,[7]
and hard for the existential theory of the reals to determine the minimum slope number of a planar drawing.[8]
Notes
2. ^{{harvtxt|Mukkamala|Szegedy|2009}}, improving an earlier result of {{harvtxt|Keszegh|Pach|Pálvölgyi|Tóth|2008}}; theorem 5.3 of {{harvtxt|Pach|Sharir|2009}}.
3. ^{{harvtxt|Mukkamala|Pálvölgyi|2012}}.
4. ^{{harvtxt|Pach|Sharir|2009}}.
5. ^{{harvtxt|Hansen|1988}}.
6. ^{{harvtxt|Formann|Hagerup|Haralambides|Kaufmann|1993}}; {{harvtxt|Eades|Hong|Poon|2010}}; {{harvtxt|Maňuch|Patterson|Poon|Thachuk|2011}}.
7. ^{{harvtxt|Garg|Tamassia|2001}}.
8. ^{{harvtxt|Hoffmann|2016}}.
References
{{refbegin|colwidth=30em}}- {{citation
| last1 = Barát | first1 = János
| last2 = Matoušek | first2 = Jiří | author2-link = Jiří Matoušek (mathematician)
| last3 = Wood | first3 = David R.
| issue = 1
| journal = Electronic Journal of Combinatorics
| mr = 2200531
| page = R3
| title = Bounded-degree graphs have arbitrarily large geometric thickness
| url = http://www.combinatorics.org/Volume_13/Abstracts/v13i1r3.html
| volume = 13
| year = 2006}}.
- {{citation
| last1 = Dujmović | first1 = Vida
| last2 = Suderman | first2 = Matthew
| last3 = Wood | first3 = David R.
| editor-last = Pach | editor-first = János | editor-link = János Pach
| contribution = Really straight graph drawings
| doi = 10.1007/978-3-540-31843-9_14
| location = Berlin
| pages = 122–132
| publisher = Springer-Verlag
| series = Lecture Notes in Computer Science
| title = Graph Drawing: 12th International Symposium, GD 2004, New York, NY, USA, September 29-October 2, 2004, Revised Selected Papers
| volume = 3383
| year = 2005| arxiv = cs/0405112}}.
- {{citation
| last1 = Eades | first1 = Peter | author1-link = Peter Eades
| last2 = Hong | first2 = Seok-Hee
| last3 = Poon | first3 = Sheung-Hung
| editor1-last = Eppstein | editor1-first = David | editor1-link = David Eppstein
| editor2-last = Gansner | editor2-first = Emden R.
| contribution = On rectilinear drawing of graphs
| doi = 10.1007/978-3-642-11805-0_23
| location = Berlin
| mr = 2680455
| pages = 232–243
| publisher = Springer
| series = Lecture Notes in Computer Science
| title = Graph Drawing: 17th International Symposium, GD 2009, Chicago, IL, USA, September 22-25, 2009, Revised Papers
| volume = 5849
| year = 2010}}.
- {{citation
| last1 = Formann | first1 = M.
| last2 = Hagerup | first2 = T.
| last3 = Haralambides | first3 = J.
| last4 = Kaufmann | first4 = M.
| last5 = Leighton | first5 = F. T. | author5-link = F. Thomson Leighton
| last6 = Symvonis | first6 = A.
| last7 = Welzl | first7 = E. | author7-link = Emo Welzl
| last8 = Woeginger | first8 = G. | author8-link = Gerhard J. Woeginger
| doi = 10.1137/0222063
| issue = 5
| journal = SIAM Journal on Computing
| mr = 1237161
| pages = 1035–1052
| title = Drawing graphs in the plane with high resolution
| volume = 22
| year = 1993}}.
- {{citation
| last1 = Garg | first1 = Ashim
| last2 = Tamassia | first2 = Roberto | author2-link = Roberto Tamassia
| doi = 10.1137/S0097539794277123
| issue = 2
| journal = SIAM Journal on Computing
| mr = 1861292
| pages = 601–625
| title = On the computational complexity of upward and rectilinear planarity testing
| volume = 31
| year = 2001}}.
- {{citation
| last = Hansen | first = Lowell J.
| issue = 1
| journal = Complex Variables, Theory and Application
| mr = 946096
| pages = 23–30
| title = On the Rodin and Sullivan ring lemma
| volume = 10
| year = 1988
| doi=10.1080/17476938808814284}}.
- {{citation
| last = Hoffmann | first = Udo
| contribution = The planar slope number
| title = Proceedings of the 28th Canadian Conference on Computational Geometry (CCCG 2016)
| year = 2016}}.
- {{citation
| last = Jamison | first = Robert E.
| doi = 10.1007/BF00147419
| issue = 1
| journal = Geometriae Dedicata
| mr = 757792
| pages = 17–34
| title = Planar configurations which determine few slopes
| volume = 16
| year = 1984}}.
- {{citation
| last1 = Keszegh | first1 = Balázs
| last2 = Pach | first2 = János | author2-link = János Pach
| last3 = Pálvölgyi | first3 = Dömötör
| editor1-last = Brandes | editor1-first = Ulrik
| editor2-last = Cornelsen | editor2-first = Sabine
| contribution = Drawing planar graphs of bounded degree with few slopes
| doi = 10.1007/978-3-642-18469-7_27
| location = Heidelberg
| mr = 2781274
| pages = 293–304
| publisher = Springer
| series = Lecture Notes in Computer Science
| title = Graph Drawing: 18th International Symposium, GD 2010, Konstanz, Germany, September 21-24, 2010, Revised Selected Papers
| volume = 6502
| year = 2011| arxiv = 1009.1315}}.
- {{citation
| last1 = Keszegh | first1 = Balázs
| last2 = Pach | first2 = János | author2-link = János Pach
| last3 = Pálvölgyi | first3 = Dömötör
| last4 = Tóth | first4 = Géza
| doi = 10.1016/j.comgeo.2007.05.003
| issue = 2
| journal = Computational Geometry: Theory and Applications
| mr = 2400539
| pages = 138–147
| title = Drawing cubic graphs with at most five slopes
| volume = 40
| year = 2008}}.
- {{citation
| last1 = Malitz | first1 = Seth
| last2 = Papakostas | first2 = Achilleas
| doi = 10.1137/S0895480193242931
| issue = 2
| journal = SIAM Journal on Discrete Mathematics
| mr = 1271989
| pages = 172–183
| title = On the angular resolution of planar graphs
| volume = 7
| year = 1994}}.
- {{citation
| last1 = Maňuch | first1 = Ján
| last2 = Patterson | first2 = Murray
| last3 = Poon | first3 = Sheung-Hung
| last4 = Thachuk | first4 = Chris
| editor1-last = Brandes | editor1-first = Ulrik
| editor2-last = Cornelsen | editor2-first = Sabine
| contribution = Complexity of finding non-planar rectilinear drawings of graphs
| doi = 10.1007/978-3-642-18469-7_28
| location = Heidelberg
| mr = 2781275
| pages = 305–316
| publisher = Springer
| series = Lecture Notes in Computer Science
| title = Graph Drawing: 18th International Symposium, GD 2010, Konstanz, Germany, September 21-24, 2010, Revised Selected Papers
| volume = 6502
| year = 2011}}.
- {{citation
| last1 = Mukkamala | first1 = Padmini
| last2 = Szegedy | first2 = Mario | author2-link = Mario Szegedy
| doi = 10.1016/j.comgeo.2009.01.005
| issue = 9
| journal = Computational Geometry: Theory and Applications
| mr = 2543806
| pages = 842–851
| title = Geometric representation of cubic graphs with four directions
| volume = 42
| year = 2009}}.
- {{citation
| last1 = Mukkamala | first1 = Padmini
| last2 = Pálvölgyi | first2 = Dömötör
| editor1-last = van Kreveld | editor1-first = Marc
| editor2-last = Speckmann | editor2-first = Bettina | editor2-link = Bettina Speckmann
| contribution = Drawing cubic graphs with the four basic slopes
| doi = 10.1007/978-3-642-25878-7_25
| pages = 254–265
| publisher = Springer
| series = Lecture Notes in Computer Science
| title = Graph Drawing: 19th International Symposium, GD 2011, Eindhoven, The Netherlands, September 21-23, 2011, Revised Selected Papers
| volume = 7034
| year = 2012| arxiv = 1106.1973}}.
- {{citation
| last1 = Pach | first1 = János | author1-link = János Pach
| last2 = Pálvölgyi | first2 = Dömötör
| issue = 1
| journal = Electronic Journal of Combinatorics
| mr = 2200545
| page = N1
| title = Bounded-degree graphs can have arbitrarily large slope numbers
| url = http://www.combinatorics.org/Volume_13/Abstracts/v13i1n1.html
| volume = 13
| year = 2006}}.
- {{citation
| last1 = Pach | first1 = János | author1-link = János Pach
| last2 = Sharir | first2 = Micha | author2-link = Micha Sharir
| contribution = 5.5 Angular resolution and slopes
| pages = 126–127
| publisher = American Mathematical Society
| series = Mathematical Surveys and Monographs
| title = Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures
| volume = 152
| year = 2009}}.
- {{citation
| last = Scott | first = P. R.
| journal = American Mathematical Monthly
| mr = 0262933
| pages = 502–505
| title = On the sets of directions determined by {{mvar|n}} points
| volume = 77
| year = 1970
| doi=10.2307/2317384}}.
- {{citation
| last1 = Wade | first1 = G. A.
| last2 = Chu | first2 = J.-H.
| doi = 10.1093/comjnl/37.2.139
| issue = 2
| journal = The Computer Journal
| pages = 139–142
| title = Drawability of complete graphs using a minimal slope set
| volume = 37
| year = 1994}}.{{refend}}
- Reverse jewel squid
- Reverse-keyed
- Reverse Koebner phenomenon
- Reverse Logic (album)
- Reverse logistics network modelling
- Reverse Marranos
- Reverse migration
- Reverse migration (bird migration)
- Reverse migration (disambiguation)
- Reverse migration (immunology)
- Reverse migration (Immunology)
- Reverse of the Medal
- Reverse Osmosis A Cappella
- Reverse Osmosis (a cappella group)
- Reverse Osmosis Water Purification Unit
- Reverse payment patent settlement
- Reverse Pharmacology
- Reverse pharmacology
- Reverse pipetting
- Reverse Polish Lisp
- Reverse post-material thesis
- Reverse Power Feeding
- Reverse power feeding
- Reverse proxies
- Reverse Psychology (album)