- See also
- Notes
- References
In functional analysis and related areas of mathematics, Smith space is a complete compactly generated locally convex space  having a compact set
having a compact set  which absorbs every other compact set
which absorbs every other compact set  (i.e.
(i.e.  for some
for some 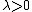 ).
).
Smith spaces are named after
[https://www.genealogy.math.ndsu.nodak.edu/id.php?id=4032 Marianne Ruth Freundlich Smith], who introduced them{{sfn|Smith|1952}} as duals to Banach spaces in some versions of duality theory for topological vector spaces. All Smith spaces are stereotype and are in the stereotype duality relations with Banach spaces:{{sfn|Akbarov|2003|p=220}}{{sfn|Akbarov|2009|p=467}}
- for any Banach space
 its stereotype dual space[1]
its stereotype dual space[1] 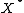 is a Smith space,
is a Smith space,
- and vice versa, for any Smith space
 its stereotype dual space
its stereotype dual space 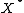 is a Banach space.
is a Banach space.
See also
- Stereotype space
- Brauner space
Notes
1. ^The stereotype dual space to a locally convex space  is the space
is the space 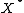 of all linear continuous functionals
of all linear continuous functionals 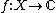 endowed with the topology of uniform convergence on totally bounded sets in
endowed with the topology of uniform convergence on totally bounded sets in  .
.
 is the space
is the space 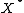 of all linear continuous functionals
of all linear continuous functionals 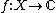 endowed with the topology of uniform convergence on totally bounded sets in
endowed with the topology of uniform convergence on totally bounded sets in  .
.References
- {{cite journal|last=Smith|first=M.F.|title=The Pontrjagin duality theorem in linear spaces|journal=Annals of Mathematics|year=1952|volume=56|issue=2|pages=248–253|doi=10.2307/1969798|jstor=1969798| ref = harv}}
- {{cite journal|last=Akbarov|first=S.S.|title=Pontryagin duality in the theory of topological vector spaces and in topological algebra|journal=Journal of Mathematical Sciences|year=2003|volume=113|issue=2|pages=179–349|doi=10.1023/A:1020929201133|url=http://www.springerlink.com/content/k62m72960101g6q2/| ref = harv}}
- {{cite journal|last=Akbarov|first=S.S.|title=Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity|journal=Journal of Mathematical Sciences|year=2009|volume=162|issue=4|pages=459–586|doi=10.1007/s10958-009-9646-1|subscription=yes|url=http://www.springerlink.com/content/u07317731010573l/| ref = harv|arxiv=0806.3205}}
- {{cite thesis |type=PhD |last=Furber |first=R.W.J. |date=2017 |title=Categorical Duality in Probability and Quantum Foundations|publisher=Radboud University| ref = harv}}
1 : Functional analysis
- Viscount of São Jorge
- Viscount of Tay and Paintland
- Viscount of the Aird and Strathglass
- Viscount of Torre de Moncorvo
- Viscount of Vilarinho de São Romão
- Viscount Ogle
- Viscount Orwell
- Viscount Oxmantown
- Viscount Perceval
- Viscount Pirrie
- Viscount Pitt
- Viscount Plumer
- Viscount Ponsonby
- Viscount Ponsonby of Imokilly
- Viscount Portal
- Viscount Preston
- Viscount Purbeck
- Viscount Pygman
- Viscount Quenington
- Viscount Raincliffe
- Viscount Ranelagh
- Viscount Raoul de Chagny
- Viscount Raymond
- Viscount Raynham
- Viscount Reading