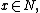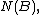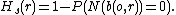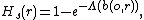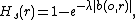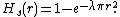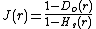请输入您要查询的百科知识：

　

词条 Spherical contact distribution function
释义

  1. Point process notation

  2. Definitions

     Spherical contact distribution function  Contact distribution function 

  3. Examples

     Poisson point process 

  4. Relationship to other functions

     Nearest neighbour function  {{mvar|J}}-function 

  5. See also

  6. References

In probability and statistics, a spherical contact distribution function, first contact distribution function,[1] or empty space function[2] is a mathematical function that is defined in relation to mathematical objects known as point processes, which are types of stochastic processes often used as mathematical models of physical phenomena representable as randomly positioned points in time, space or both.[1][3] More specifically, a spherical contact distribution function is defined as probability distribution of the radius of a sphere when it first encounters or makes contact with a point in a point process. This function can be contrasted with the nearest neighbour function, which is defined in relation to some point in the point process as being the probability distribution of the distance from that point to its nearest neighbouring point in the same point process.

The spherical contact function is also referred to as the contact distribution function,[2] but some authors[1] define the contact distribution function in relation to a more general set, and not simply a sphere as in the case of the spherical contact distribution function.

Spherical contact distribution functions are used in the study of point processes[2][3][4] as well as the related fields of stochastic geometry[1] and spatial statistics,[2][5] which are applied in various scientific and engineering disciplines such as biology, geology, physics, and telecommunications.[1][3][6][7]

Point process notation

{{Main|Point process notation}}

Point processes are mathematical objects that are defined on some underlying mathematical space. Since these processes are often used to represent collections of points randomly scattered in space, time or both, the underlying space is usually d-dimensional Euclidean space denoted here by 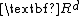, but they can be defined on more abstract mathematical spaces.[4]

Point processes have a number of interpretations, which is reflected by the various types of point process notation.[1][7] For example, if a point belongs to or is a member of a point process, denoted by 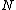, then this can be written as:[1]

and represents the point process being interpreted as a random set. Alternatively, the number of points of 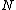located in some Borel set 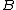is often written as:[1][5][6]

which reflects a random measure interpretation for point processes. These two notations are often used in parallel or interchangeably.[1][5][6]

Definitions

Spherical contact distribution function

The spherical contact distribution function is defined as:

where b(o,r) is a ball with radius r centered at the origin o. In other words, spherical contact distribution function is the probability there are no points from the point process located in a hyper-sphere of radius r.

Contact distribution function

The spherical contact distribution function can be generalized for sets other than the (hyper-)sphere in 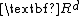. For some Borel set 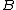with positive volume (or more specifically, Lebesgue measure), the contact distribution function (with respect to 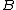) for 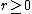is defined by the equation:[1]

Examples

Poisson point process

For a Poisson point process 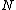on 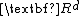with intensity measure 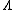this becomes

which for the homogeneous case becomes

where 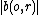denotes the volume (or more specifically, the Lebesgue measure) of the ball of radius . In the plane 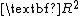, this expression simplifies to

Relationship to other functions

Nearest neighbour function

In general, the spherical contact distribution function and the corresponding nearest neighbour function are not equal. However, these two functions are identical for Poisson point processes.[1] In fact, this characteristic is due to a unique property of Poisson processes and their Palm distributions, which forms part of the result known as the Slivnyak-Mecke[6] or Slivnyak's theorem.[2]

{{mvar|J}}-function

The fact that the spherical distribution function {{mvar| Hs(r)}} and nearest neighbour function {{mvar| Do(r)}} are identical for the Poisson point process can be used to statistically test if point process data appears to be that of a Poisson point process. For example, in spatial statistics the {{mvar|J}}-function is defined for all {{mvar|r}} ≥ 0 as:[1]

For a Poisson point process, the {{mvar|J}} function is simply {{math|J(r)}}=1, hence why it is used as a non-parametric test for whether data behaves as though it were from a Poisson process. It is, however, thought possible to construct non-Poisson point processes for which {{math|J(r)}}=1,[8] but such counterexamples are viewed as somewhat 'artificial' by some and exist for other statistical tests.[9]

More generally, {{mvar|J}}-function serves as one way (others include using factorial moment measures[2]) to measure the interaction between points in a point process.[1]

See also

  • Nearest neighbour function
  • Factorial moment measure
  • Moment measure

References

{{notelist}}
1. ^1 2 3 4 5 6 7 8 9 10 11 12 D. Stoyan, W. S. Kendall, J. Mecke, and L. Ruschendorf. Stochastic geometry and its applications, volume 2. Wiley Chichester, 1995.
2. ^1 2 3 4 5 A. Baddeley, I. Bárány, and R. Schneider. Spatial point processes and their applications. Stochastic Geometry: Lectures given at the CIME Summer School held in Martina Franca, Italy, September 13--18, 2004, pages 1--75, 2007.
3. ^1 2 D. J. Daley and D. Vere-Jones. An introduction to the theory of point processes. Vol. I. Probability and its Applications (New York). Springer, New York, second edition, 2003.
4. ^1 D. J. Daley and D. Vere-Jones. An introduction to the theory of point processes. Vol. {II}. Probability and its Applications (New York). Springer, New York, second edition, 2008.
5. ^1 2 J. Moller and R. P. Waagepetersen. Statistical inference and simulation for spatial point processes. CRC Press, 2003.
6. ^1 2 3 F. Baccelli and B. Błaszczyszyn. Stochastic Geometry and Wireless Networks, Volume I – Theory, volume 3, No 3-4 of Foundations and Trends in Networking. NoW Publishers, 2009.
7. ^1 F. Baccelli and B. Błaszczyszyn. Stochastic Geometry and Wireless Networks, Volume II – Applications, volume 4, No 1-2 of Foundations and Trends in Networking. NoW Publishers, 2009.
8. ^{{cite journal| author=Bedford, T, Van den Berg, J| title=A remark on the Van Lieshout and Baddeley J-function for point processes| journal=Advances in Applied Probability| year=1997| pages=19–25| publisher=JSTOR}}
9. ^{{cite journal| author=Foxall, Rob, Baddeley, Adrian| title=Nonparametric measures of association between a spatial point process and a random set, with geological applications| journal=Journal of the Royal Statistical Society, Series C| year=2002| volume=51| number=2| pages=165–182| publisher=Wiley Online Library| doi=10.1111/1467-9876.00261}}

2 : Stochastic processes|Spatial data analysis
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/15 13:11:24