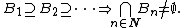“Spherically complete field”的意思、由来-开放百科全书

词条

Spherically complete field

释义

Examples
References

In mathematics, a field K with an absolute value is called spherically complete if the intersection of every decreasing sequence of balls (in the sense of the metric induced by the absolute value) is nonempty:

The definition can be adapted also to a field K with a valuation v taking values in an arbitrary ordered abelian group: (K,v) is spherically complete if every collection of balls that is totally ordered by inclusion has a nonempty intersection.

Spherically complete fields are important in nonarchimedean functional analysis, since many results analogous to theorems of classical functional analysis require the base field to be spherically complete.

Examples

Any locally compact field is spherically complete. This includes, in particular, the fields Q_p of p-adic numbers, and any of their finite extensions.
On the other hand, C_p, the completion of the algebraic closure of Q_p, is not spherically complete.^[1]
Any field of Hahn series is spherically complete.

References

1. ^Robert, [https://books.google.de/books?id=H6sq_x2-DgoC&PA143 p. 143]

{{cite book |title=Nonarchimedean Functional Analysis
|last=Schneider
|first=Peter
|year=2001
|publisher=Springer
|isbn=3-540-42533-0}}{{mathanalysis-stub}}

2 : Algebra|Functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。