“Sylvester matroid”的意思、由来-开放百科全书

In matroid theory, a Sylvester matroid is a matroid in which every pair of elements belongs to a three-element circuit (a triangle) of the matroid.^[1]^[2]

Example

The

-point line (i.e., the rank 2 uniform matroid on

elements,

) is a Sylvester matroid because every pair of elements is a basis and every triple is a circuit.

A Sylvester matroid of rank three may be formed from any Steiner triple system, by defining the lines of the matroid to be the triples of the system. Sylvester matroids of rank three may also be formed from Sylvester–Gallai configurations, configurations of points and lines (in non-Euclidean spaces) with no two-point line. For example, the Fano plane and the Hesse configuration give rise to Sylvester matroids with seven and nine elements respectively, and may be interpreted either as Steiner triple systems or as Sylvester–Gallai configurations.

Properties

A Sylvester matroid with rank

must have at least

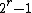elements; this bound is tight only for the projective spaces over GF(2), of which the Fano plane is an example.^[3]

In a Sylvester matroid, every independent set can be augmented by one more element to form a circuit of the matroid.^[1]^[4]

Sylvester matroids cannot be represented over the real numbers (this is the Sylvester–Gallai theorem), nor can they be oriented.^[5]

History

Sylvester matroids were studied and named by {{harvtxt|Murty|1969}} after James Joseph Sylvester, because they violate the Sylvester–Gallai theorem (for points and lines in the Euclidean plane, or in higher-dimensional Euclidean spaces) that for every finite set of points there is a line containing only two of the points.

References

1. ^¹{{citation | last = Murty | first = U. S. R. | authorlink = U. S. R. Murty | contribution = Sylvester matroids | location = New York | mr = 0255432 | pages = 283–286 | publisher = Academic Press | title = Recent Progress in Combinatorics (Proc. Third Waterloo Conf. on Combinatorics, 1968) | year = 1969}}.
2. ^{{citation | last = Welsh | first = D. J. A. | isbn = 9780486474397 | page = 297 | publisher = Courier Dover Publications | title = Matroid Theory | year = 2010}}.
3. ^{{citation | last = Murty | first = U. S. R. | doi = 10.1007/BF01817744 | journal = Aequationes Mathematicae | mr = 0265186 | pages = 44–50 | title = Matroids with Sylvester property | volume = 4 | year = 1970}}.
4. ^{{citation | last1 = Bryant | first1 = V. W. | last2 = Dawson | first2 = J. E. | last3 = Perfect | first3 = Hazel | issue = 3 | journal = Compositio Mathematica | mr = 511749 | pages = 339–351 | title = Hereditary circuit spaces | url = http://www.numdam.org/item?id=CM_1978__37_3_339_0 | volume = 37 | year = 1978}}.
5. ^{{citation | last = Ziegler | first = Günter M. | author-link = Günter M. Ziegler | doi = 10.1007/BF00181199 | issue = 3 | journal = Geometriae Dedicata | mr = 1112674 | pages = 365–371 | title = Some minimal non-orientable matroids of rank three | volume = 38 | year = 1991}}.