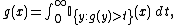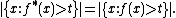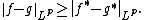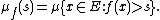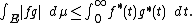“Symmetric decreasing rearrangement”的意思、由来-开放百科全书

词条

Symmetric decreasing rearrangement

释义

Definition for sets
Definition for functions
Properties
Applications
Nonsymmetric decreasing rearrangment
See also
References

In mathematics, the symmetric decreasing rearrangement of a function is a function which is symmetric and decreasing, and whose level sets are of the same size as those of the original function.^[1]

Definition for sets

Given a measurable set, , in Rⁿ one can obtain the symmetric rearrangement of , called 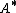, by

where is the volume of the unit ball and where is the volume (i.e., the Lebesgue measure) of . Notice that this is just the ball centered at the origin whose volume is the same as that of the set .

Definition for functions

The rearrangement of a non-negative, measurable real-valued function whose level sets 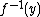() have finite measure is

where denotes the indicator function of the set A.

In words, the value of gives the height t for which the radius of the symmetric

rearrangement of is equal to x. We have the following motivation for this definition. Because the identity

holds for any non-negative function , the above definition is the unique definition that forces the identity 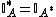to hold.

Properties

The function is a symmetric and decreasing function whose level sets have the same measure as the level sets of , i.e.

If is a function in , then

The Hardy–Littlewood inequality holds, i.e.

Further, the Pólya–Szegő inequality holds. This says that if and if then

The symmetric decreasing rearrangement is order preserving and decreases distance, i.e.

and

Applications

The Pólya–Szegő inequality yields, in the limit case, with , the isoperimetric inequality. Also, one can use some relations with harmonic functions to prove the Rayleigh–Faber–Krahn inequality.

Nonsymmetric decreasing rearrangment

We can also define f* as a function on the nonnegative real numbers rather than on all of Rⁿ.^[2] Let (E,μ) be any σ-finite measure space, and let be a measurable function that takes only finite (i.e., real) values μ-a.e. (where "μ-a.e." means except possibly on a set of μ-measure zero). We define the distribution function 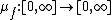by the rule

We can now define the decreasing rearrangment (or, sometimes, nonincreasing rearrangement of f as the function and the rule

Note that this version of the decreasing rearrangement is not symmetric, as it is only defined on the nonnegative real numbers. However, it inherits many of the same properties listed above as the symmetric version. Namely:

f and f* are equimeasurable, i.e. they have the same distribution function.

The Hardy-Littlewood inequality holds, i.e.

μ-a.e. implies .

for all real numbers a.

for all .

μ-a.e. implies .

for all positive real numbers p.

The (nonsymmetric) decreasing rearrangement function arises often in the theory of rearrangement-invariant Banach function spaces. Especially important is the following:

Luxemburg Representation Theorem. Let be a rearrangement-invariant Banach function norm over a resonant measure space . Then there exists a (possibly not unique) rearrangement-invariant function norm on such that for all nonnegative measurable functions which are finite-valued μ-a.e.

Note that the definitions of all the terminology in the above theorem (i.e., Banach function norms, rearrangement-invariant Banach function spaces, and resonant measure spaces) can be found in sections 1 and 2 of Bennett and Sharpley's book (cf. the references below).

References

1. ^{{cite book|last1=Lieb|first1=Elliott|authorlink1=Elliott H. Lieb|last2=Loss|first2=Michael|author2-link=Michael Loss|title=Analysis|year=2001|edition=2nd|publisher=American Mathematical Society|series=Graduate Studies in Mathematics|volume=14|isbn=978-0821827833}}
2. ^{{cite book|last1=Bennett|first1=Colin|last2=Sharpley|first2=Robert|title=Interpolation of Operators|year=1988|isbn=978-0-120-88730-9}}

2 : Multivariable calculus|Real analysis

随便看