“Tangent space to a functor”的意思、由来-开放百科全书

词条

Tangent space to a functor

释义

References

In algebraic geometry, the tangent space to a functor generalizes the classical construction of a tangent space such as the Zariski tangent space. The construction is based on the following observation.^[1] Let X be a scheme over a field k.

To give a -point of X is the same thing as to give a k-rational point p of X (i.e., the residue field of p is k) together with an element of ; i.e., a tangent vector at p.

(To see this, use the fact that any local homomorphism 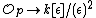must be of the form

)

Let F be a functor from the category of k-algebras to the category of sets. Then, for any k-point 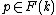, the fiber of 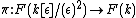over p is called the tangent space to F at p.^[2]

The tangent space may be given the structure of a vector space over k. If F is a scheme X over k (i.e., 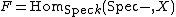), then each v as above may be identified with a derivation at p and this gives the identification of 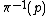with the space of derivations at p and we recover the usual construction.

The construction may be thought of as defining an analog of the tangent bundle in the following way.^[3] Let 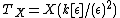. Then, for any morphism of schemes over k, one sees 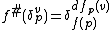; this shows that the map 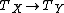that f induces is precisely the differential of f under the above identification.

References

1. ^{{harvnb|Hartshorne|1977|loc=Exercise II 2.8}}
2. ^{{harvnb|Eisenbud–Harris|1998|loc=VI.1.3}}
3. ^{{harvnb|Borel|1991|loc=AG 16.2}}

A. Borel, Linear algebraic groups
{{cite book

| author = David Eisenbud
|author2=Joe Harris |authorlink2=Joe Harris (mathematician)
| year = 1998
| title = The Geometry of Schemes
| publisher = Springer-Verlag
| isbn = 0-387-98637-5
| zbl = 0960.14002
}}

{{Hartshorne AG}}

1 : Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。