“Tietze extension theorem”的意思、由来-开放百科全书

词条

Tietze extension theorem

释义

Formal statement
History
Equivalent statements
Variations
See also
References
External links

In topology, the Tietze extension theorem (also known as the Tietze–Urysohn–Brouwer extension theorem) states that continuous functions on a closed subset of a normal topological space can be extended to the entire space, preserving boundedness if necessary.

Formal statement

If X is a normal topological space and

is a continuous map from a closed subset A of X into the real numbers carrying the standard topology, then there exists a continuous map

with F(a) = f(a) for all a in A. Moreover, F may be chosen such that , i.e., if f is bounded, F may be chosen to be bounded (with the same bound as f). F is called a continuous extension of f.

History

L. E. J. Brouwer and Henri Lebesgue proved a special case of the theorem, when X is a finite-dimensional real vector space. Heinrich Tietze extended it to all metric spaces, and Paul Urysohn proved the theorem as stated here, for normal topological spaces.^[1]^[2]

Equivalent statements

This theorem is equivalent to Urysohn's lemma (which is also equivalent to the normality of the space) and is widely applicable, since all metric spaces and all compact Hausdorff spaces are normal. It can be generalized by replacing R with R^J for some indexing set J, any retract of R^J, or any normal absolute retract whatsoever.

Variations

If X is a metric space, A a non-empty subset of X and 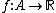is a Lipschitz continuous function with Lipschitz constant K, then f can be extended to a Lipschitz continuous function 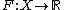with same constant K.

This theorem is also valid for Hölder continuous functions, that is, if 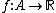is Hölder continuous function, f can be extended to a Hölder continuous function 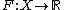with the same constant.^[3]

Another variant (in fact, generalization) of Tietze's theorem is due to Z. Ercan:^[4]

Let A be a closed subset of a topological space X. If 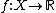is an

upper semicontinuous function, 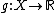a lower semicontinuous function

and 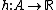a continuous function such that f(x)≤g(x) for

each x∈X and f(a)≤h(a)≤g(a) for each a∈A, then there is a continuous

extension 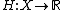of h such that f(x)≤H(x)≤g(x) for

each x∈X.

This theorem is also valid with some additional hypothesis if R is replaced by a general locally solid Riesz space.^[4]

References

1. ^{{springer|title=Urysohn-Brouwer lemma|id=p/u095860}}
2. ^{{citation|first=Paul|last=Urysohn|authorlink=Pavel Samuilovich Urysohn|journal=Mathematische Annalen|year=1925|volume=94|issue=1|pages=262–295|title=Über die Mächtigkeit der zusammenhängenden Mengen|doi=10.1007/BF01208659}}.
3. ^{{cite journal|last1=McShane|first1=E. J.|title=Extension of range of functions|journal=Bulletin of the American Mathematical Society|date=1 December 1934|volume=40|issue=12|pages=837–843|doi=10.1090/S0002-9904-1934-05978-0}}
4. ^¹{{cite journal|last1=Zafer|first1=Ercan|title=Extension and Separation of Vector Valued Functions|journal=Turkish Journal of Mathematics|date=1997|volume=21|issue=4|pages=423–430|url=http://journals.tubitak.gov.tr/math/issues/mat-97-21-4/mat-21-4-4-e2104-04.pdf}}

External links

Weisstein, Eric W. "Tietze's Extension Theorem." From MathWorld
{{planetmath reference|id=4215|title=Tietze extension theorem}}
{{planetmath reference|id=5566|title=Proof of Tietze extension theorem}}
Mizar system proof: http://mizar.org/version/current/html/tietze.html#T23
{{citation | first =Edmond| last =Bonan| title =Relèvements-Prolongements à valeurs dans les espaces de Fréchet| journal = Comptes Rendus de l'Académie des Sciences, Série I|volume =272| year =1971 | pages = 714–717}}.

2 : Continuous mappings|Theorems in topology

随便看