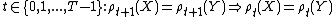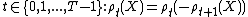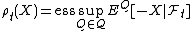1. Time consistency and financial risk
    Mathematical definition  Equivalent definitions  Construction  Examples  Value at risk and average value at risk  Time consistent alternative  Dynamic superhedging price  Dynamic entropic risk   Continuous time  

2. References

Time consistency in the context of finance is the property of not having mutually contradictory evaluations of risk at different points in time. This property implies that if investment A is considered riskier than B at some future time, then A will also be considered riskier than B at every prior time.

Time consistency and financial risk

Time consistency is a property in financial risk related to dynamic risk measures. The purpose of the time the consistent property is to categorize the risk measures which satisfy the condition that if portfolio (A) is riskier than portfolio (B) at some time in the future, then it is guaranteed to be riskier at any time prior to that point. This is an important property since if it were not to hold then there is an event (with probability of occurring greater than 0) such that B is riskier than A at time although it is certain that A is riskier than B at time 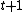. As the name suggests a time inconsistent risk measure can lead to inconsistent behavior in financial risk management.

Mathematical definition

A dynamic risk measure 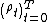on is time consistent if and implies .^[1]

Equivalent definitions

Equality

For all

Recursive

For all

Acceptance Set

For all where is the time acceptance set and ^[2]

Cocycle condition (for

//convex risk measure">convex risk measures)

For all where is the minimal penalty function (where is an acceptance set and denotes the essential supremum) at time and .^[3]

Construction

Due to the recursive property it is simple to construct a time consistent risk measure. This is done by composing one-period measures over time. This would mean that:

• 
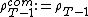
• ^[1]

Examples

Value at risk and average value at risk

Both dynamic value at risk and dynamic average value at risk are not a time consistent risk measures.

Time consistent alternative

The time consistent alternative to the dynamic average value at risk with parameter at time t is defined by

such that .^[4]

Dynamic superhedging price

The dynamic superhedging price is a time consistent risk measure.^[5]

Dynamic entropic risk

The dynamic entropic risk measure is a time consistent risk measure if the risk aversion parameter is constant.^[5]

Continuous time

In continuous time, a time consistent coherent risk measure can be given by:

for a sublinear choice of function where denotes a g-expectation. If the function is convex, then the corresponding risk measure is convex.^[6]

References

• 1826 United States House of Representatives elections in New York
• 1826 United States Senate election in Massachusetts
• 1826–1837 cholera pandemic
• 18278 Drymas
• 1827 AHS
• 1827 in birding and ornithology
• 1827 in France
• 1827 in India
• 1827 in Norway
• 1827 in sports
• 1827 United States Senate election in New York
• 18281 Tros
• 18282 Ilos
• 18284 Tsereteli
• 18286 Kneipp
• 18287 Verkin
• 18288 Nozdrachev
• 1828 AHS
• 1828 and 1829 United States Senate elections
• 1828 in birding and ornithology
• 1828 in France
• 1828 in Norway
• 1828 in paleontology
• 1828 in sports
• 1828 Kashirina