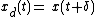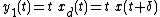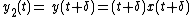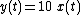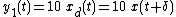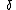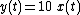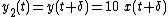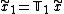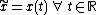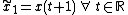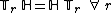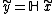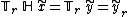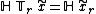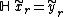“Time-invariant system”的意思、由来-开放百科全书

词条

Time-invariant system

释义

Simple example
Formal example
Abstract example
See also
References

A time-invariant (TIV) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends only indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system".

Mathematically speaking, "time-invariance" of a system is the following property:^[1]{{rp|p. 50}}

Given a system with a time-dependent output function , and a time-dependent input function ; the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship between the input function and the output function is constant with respect to time :

In the language of signal processing, this property can be satisfied if the transfer function of the system is not a direct function of time except as expressed by the input and output.

In the context of a system schematic, this property can also be stated as follows:

If a system is time-invariant then the system block commutes with an arbitrary delay.

If a time-invariant system is also linear, it is the subject of linear time-invariant theory (linear time-invariant) with direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. Nonlinear time-invariant systems lack a comprehensive, governing theory. Discrete time-invariant systems are known as shift-invariant systems. Systems which lack the time-invariant property are studied as time-variant systems.

Simple example

To demonstrate how to determine if a system is time-invariant, consider the two systems:

System A:
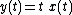
System B:

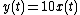
Since system A explicitly depends on t outside of and , it is not time-invariant. System B, however, does not depend explicitly on t so it is time-invariant.

Formal example

A more formal proof of why systems A and B above differ is now presented.

To perform this proof, the second definition will be used.

System A:

Start with a delay of the input

Now delay the output by

Clearly , therefore the system is not time-invariant.

System B:

Start with a delay of the input

Now delay the output by

Clearly , therefore the system is time-invariant.

More generally, the relationship between the input and output is 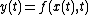, and its variation with time is

.

For time-invariant systems, the system properties remain constant with time, 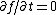. Applied to Systems A and B above:

in general, so not time-invariant

so time-invariant.

Abstract example

We can denote the shift operator by 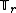where is the amount by which a vector's index set should be shifted. For example, the "advance-by-1" system

can be represented in this abstract notation by

where is a function given by

with the system yielding the shifted output

So 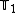is an operator that advances the input vector by 1.

Suppose we represent a system by an operator 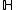. This system is time-invariant if it commutes with the shift operator, i.e.,

If our system equation is given by

then it is time-invariant if we can apply the system operator 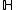on followed by the shift operator 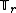, or we can apply the shift operator 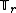followed by the system operator 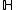, with the two computations yielding equivalent results.

Applying the system operator first gives

Applying the shift operator first gives

If the system is time-invariant, then

References

1. ^{{cite book | first1=Alan | last1=Oppenheim | first2=Alan | last2=Willsky | title=Signals and Systems (second edition)| publisher=Prentice Hall | year=1997}}

2 : Control theory|Signal processing

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Simple example

Formal example

Abstract example

See also

References