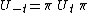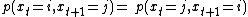“Time reversibility”的意思、由来-开放百科全书

A mathematical or physical process is time-reversible if the dynamics of the process remain well-defined when the sequence of time-states is reversed.

A deterministic process is time-reversible if the time-reversed process satisfies the same dynamic equations as the original process; in other words, the equations are invariant or symmetrical under a change in the sign of time. A stochastic process is reversible if the statistical properties of the process are the same as the statistical properties for time-reversed data from the same process.

Mathematics

In mathematics, a dynamical system is time-reversible if the forward evolution is one-to-one, so that for every state there exists a transformation (an involution) π which gives a one-to-one mapping between the time-reversed evolution of any one state and the forward-time evolution of another corresponding state, given by the operator equation:

Any time-independent structures (e.g. critical points or attractors) which the dynamics give rise to must therefore either be self-symmetrical or have symmetrical images under the involution π.

Physics

In physics, the laws of motion of classical mechanics exhibit time reversibility, as long as the operator π reverses the conjugate momenta of all the particles of the system, i.e.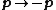

(T-symmetry).

In quantum mechanical systems, however, the weak nuclear force is not invariant under T-symmetry alone; if weak interactions are present reversible dynamics are still possible, but only if the operator π also reverses the signs of all the charges and the parity of the spatial co-ordinates (C-symmetry and P-symmetry). This reversibility of several linked properties is known as CPT symmetry.

Thermodynamic processes can be reversible or irreversible, depending on the change in entropy during the process.

Stochastic processes

A stochastic process is time-reversible if the joint probabilities of the forward and reverse state sequences are the same for all sets of time increments { τ_s }, for s = 1, ..., k for any k:^[1]

A univariate stationary Gaussian process is time-reversible. Markov processes can only be reversible if their stationary distributions have the property of detailed balance:

Kolmogorov's criterion defines the condition for a Markov chain or continuous-time Markov chain to be time-reversible.

Time reversal of numerous classes of stochastic processes has been studied, including Lévy processes,^[2] stochastic networks (Kelly's lemma),^[3] birth and death processes,^[4] Markov chains,^[5] and piecewise deterministic Markov processes.^[6]

Waves and optics

Time reversal method works based on the linear reciprocity of the wave equation, which states that the time reversed solution of a wave equation is also a solution to the wave equation since standard wave equations only contain even derivatives of the unknown variables.^[7] Thus, the wave equation is symmetrical under time reversal, so the time reversal of any valid solution is also a solution. This means that a wave's path through space is valid when travelled in either direction.

Time reversal signal processing is a process in which this property is used to reverse a received signal; this signal is then re-emitted and a temporal compression occurs, resulting in a reverse of the initial excitation waveform being played at the initial source.

See also

Notes

1. ^Tong (1990), Section 4.4
2. ^{{Cite journal | last1 = Jacod | first1 = J. | last2 = Protter | first2 = P. | doi = 10.1214/aop/1176991776 | title = Time Reversal on Levy Processes | journal = The Annals of Probability | volume = 16 | issue = 2 | pages = 620 | year = 1988 | jstor = 2243828| pmid = | pmc = }}
3. ^{{Cite journal | last1 = Kelly | first1 = F. P. | authorlink1 = Frank Kelly (mathematician)| title = Networks of Queues | journal = Advances in Applied Probability | volume = 8 | issue = 2 | pages = 416–432 | doi = 10.2307/1425912 | jstor = 1425912| year = 1976 | pmid = | pmc = }}
4. ^{{Cite journal | last1 = Tanaka | first1 = H. | doi = 10.3836/tjm/1270133555 | title = Time Reversal of Random Walks in One-Dimension | journal = Tokyo Journal of Mathematics | volume = 12 | pages = 159–174 | year = 1989 | pmid = | pmc = }}
5. ^{{cite book | title = Markov Chains | first = J. R. | last= Norris | authorlink = James R. Norris | publisher = Cambridge University Press | year =1998 | isbn = 978-0521633963}}
6. ^{{Cite journal | last1 = Löpker | first1 = A. | last2 = Palmowski | first2 = Z. | doi = 10.1214/EJP.v18-1958 | title = On time reversal of piecewise deterministic Markov processes | journal = Electronic Journal of Probability | volume = 18 | year = 2013 | arxiv = 1110.3813| pmid = | pmc = }}
7. ^{{cite journal|last1=Parvasi|first1=Seyed Mohammad|last2=Ho|first2=Siu Chun Michael|last3=Kong|first3=Qingzhao|last4=Mousavi|first4=Reza|last5=Song|first5=Gangbing|title=Real time bolt preload monitoring using piezoceramic transducers and time reversal technique—a numerical study with experimental verification|journal=Smart Materials and Structures|date=19 July 2016|volume=25|issue=8|pages=085015|doi=10.1088/0964-1726/25/8/085015|language=en|issn=0964-1726|bibcode=2016SMaS...25h5015P}}

Mathematics

Physics

Stochastic processes

Waves and optics

See also

Notes

References