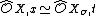1. Definition

2. Examples
     Tits' buildings  

3. See also

4. References

5. External links

In algebraic geometry, a toroidal embedding is an open embedding of algebraic varieties that locally looks like the embedding of the open torus into a toric variety. The notion was introduced by Mumford to prove the existence of semistable reductions of algebraic varieties over one-dimensional bases.

Definition

Let X be a normal variety over an algebraically closed fiel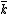d and 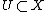a smooth open subset. Then 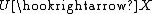is called a toroidal embedding if for every closed point x of X, there is an isomorphism of local 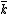-algebras:

for some affine toric variety 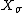with a torus T and a point t such that the above isomorphism takes the ideal of 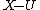to that of .

Let X be a normal variety over a field k. An open embedding 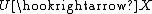is said to a toroidal embedding if 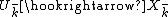is a toroidal embedding.

Examples

Tits' buildings

See also

• tropical compactification

References

• {{Citation | last1=Kempf | first1=G. | last2=Knudsen | first2=Finn Faye | last3=Mumford | first3=David | author3-link=David Mumford | last4=Saint-Donat | first4=B. | title=Toroidal embeddings. I | publisher=Springer-Verlag | location=Berlin, New York | series=Lecture Notes in Mathematics | doi= 10.1007/BFb0070318 | mr=0335518 | year=1973 | volume=339}}
• Abramovich, D., Denef, J. & Karu, K.: Weak toroidalization over non-closed fields. manuscripta math. (2013) 142: 257. https://doi.org/10.1007/s00229-013-0610-5

External links

• http://mathoverflow.net/questions/124367/toroidal-embedding

• Las Positas Community College
• Las Pozas
• Laspra
• Las Praderas Tournament
• LA's Promise
• Las Puertitas del senor Lopez
• Laspuna
• Laspuna, Huesca
• Laspuna, Spain
• Las Qorey
• Lasqueti, British Columbia
• Las, qu'i non sun sparvir, astur
• Las Raices tunnel
• LASRE
• Las Reinas Del Pueblo
• Lasren mac Feradaig
• Lasren of Iona
• Las Rosas, Chiapas
• Las Rozas CF
• Lasrs
• Las Ruedas, New Mexico
• LASS1
• LASS2
• Lassa
• Lassaba