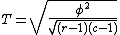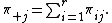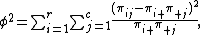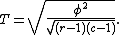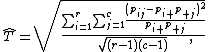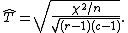“Tschuprow's T”的意思、由来-开放百科全书

词条

Tschuprow's T

释义

Definition
Properties Estimation
See also
References

Tschuprow's T

In statistics, Tschuprow's T is a measure of association between two nominal variables, giving a value between 0 and 1 (inclusive). It is closely related to Cramér's V, coinciding with it for square contingency tables.

It was published by Alexander Tschuprow (alternative spelling: Chuprov) in 1939.^[1]

Definition

For an r × c contingency table with r rows and c columns, let 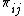be the proportion of the population in cell and let

and

Then the mean square contingency is given as

and Tschuprow's T as

Properties

T equals zero if and only if independence holds in the table, i.e., if and only if 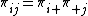. T equals one if and only there is perfect dependence in the table, i.e., if and only if for each i there is only one j such that 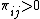and vice versa. Hence, it can only equal 1 for square tables. In this it differs from Cramér's V, which can be equal to 1 for any rectangular table.

Estimation

If we have a multinomial sample of size n, the usual way to estimate T from the data is via the formula

where 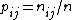is the proportion of the sample in cell . This is the empirical value of T. With the Pearson chi-square statistic, this formula can also be written as

References

1. ^Tschuprow, A. A. (1939) Principles of the Mathematical Theory of Correlation; translated by M. Kantorowitsch. W. Hodge & Co.

Liebetrau, A. (1983). Measures of Association (Quantitative Applications in the Social Sciences). Sage Publications

1 : Summary statistics for contingency tables

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Properties

Estimation

See also

References