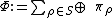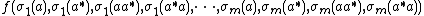1. Formal definition and properties
    States of Φ(A)  Bounded functionals of Φ(A)  Ideals of Φ(A)  Representations of A  Ultraweakly continuous, and singular components 

2. Applications
    Christensen–Haagerup principle 

3. See also

4. References

In the theory of C*-algebras, the universal representation of a C*-algebra is a faithful representation which is the direct sum of the GNS representations corresponding to the states of the C*-algebra. The various properties of the universal representation are used to obtain information about the ideals and quotients of the C*-algebra. The close relationship between an arbitrary representation of a C*-algebra and its universal representation can be exploited to obtain several criteria for determining whether a linear functional on the algebra is ultraweakly continuous. The method of using the properties of the universal representation as a tool to prove results about the C*-algebra and its representations is commonly referred to as universal representation techniques in the literature.

Formal definition and properties

Definition. Let A be a C*-algebra with state space S. The representation

on the Hilbert space is known as the universal representation of A.

As the universal representation is faithful, A is *-isomorphic to the C*-subalgebra Φ(A) of B(H_Φ).

States of Φ(A)

With τ a state of A, let π_τ denote the corresponding GNS representation on the Hilbert space H_τ. Using the notation defined here, τ is ω_x ∘ π_τ for a suitable unit vector x(=x_τ) in H_τ. Thus τ is ω_y ∘ Φ, where y is the unit vector ∑_ρ∈S ⊕y_ρ in H_Φ, defined by y_τ=x, y_ρ=0(ρ≠τ). Since the mapping τ → τ ∘ Φ⁻¹ takes the state space of A onto the state space of Φ(A), it follows that each state of Φ(A) is a vector state.

Bounded functionals of Φ(A)

Let Φ(A)⁻ denote the weak-operator closure of Φ(A) in B(H_Φ). Each bounded linear functional ρ on Φ(A) is weak-operator continuous and extends uniquely preserving norm, to a weak-operator continuous linear functional {{overline|ρ}} on the von Neumann algebra Φ(A)⁻. If ρ is hermitian, or positive, the same is true of {{overline|ρ}}. The mapping ρ → {{overline|ρ}} is an isometric isomorphism from the dual space Φ(A)^* onto the predual of Φ(A)⁻. As the set of linear functionals determining the weak topologies coincide, the weak-operator topology on Φ(A)⁻ coincides with the ultraweak topology. Thus the weak-operator and ultraweak topologies on Φ(A) both coincide with the weak topology of Φ(A) obtained from its norm-dual as a Banach space.

Ideals of Φ(A)

If K is a convex subset of Φ(A), the ultraweak closure of K (denoted by K⁻)coincides with the strong-operator, weak-operator closures of K in B(H_Φ). The norm closure of K is Φ(A) ∩ K⁻. One can give a description of norm-closed left ideals in Φ(A) from the structure theory of ideals for von Neumann algebras, which is relatively much more simple. If K is a norm-closed left ideal in Φ(A), there is a projection E in Φ(A)⁻ such that

If K is a norm-closed two-sided ideal in Φ(A), E lies in the center of Φ(A)⁻.

Representations of A

If π is a representation of A, there is a projection P in the center of Φ(A)⁻ and a *-isomorphism α from the von Neumann algebra Φ(A)⁻P onto π(A)⁻ such that π(a) = α(Φ(a)P) for each a in A. This can be conveniently captured in the commutative diagram below :

Here ψ is the map that sends a to aP, α₀ denotes the restriction of α to Φ(A)P, ι denotes the inclusion map.

As α is ultraweakly bicontinuous, the same is true of α₀. Moreover, ψ is ultraweakly continuous, and is a *-isomorphism if π is a faithful representation.

Ultraweakly continuous, and singular components

Let A be a C*-algebra acting on a Hilbert space H. For ρ in A^* and S in Φ(A)⁻, let Sρ in A^* be defined by Sρ(a) = {{overline|ρ∘Φ⁻¹}}(Φ(a)S) for all a in A. If P is the projection in the above commutative diagram when π:A → B(H) is the inclusion mapping, then ρ in A^* is ultraweakly continuous if and only if ρ = Pρ. A functional ρ in A^* is said to be singular if Pρ = 0.

Each ρ in A^* can be uniquely expressed in the form ρ=ρ_u+ρ_s, with ρ_u ultraweakly continuous and ρ_s singular. Moreover, ||ρ||=||ρ_u||+||ρ_s|| and if ρ is positive, or hermitian, the same is true of ρ_u, ρ_s.

Applications

Christensen–Haagerup principle

Let f and g be continuous, real-valued functions on C^4m and C⁴ⁿ, respectively, σ₁, σ₂, ..., σ_m be ultraweakly continuous, linear functionals on a von Neumann algebra R acting on the Hilbert space H, and ρ₁, ρ₂, ..., ρ_n be bounded linear functionals on R such that, for each a in R,

Then the above inequality holds if each ρ_j is replaced by its ultraweakly continuous component (ρ_j)_u.

See also

References

• Kadison, Richard, Fundamentals of the Theory of Operator Algebras, Vol. I : Elementary Theory, American Mathematical Society. {{ISBN|978-0821808191}}.
• Kadison, Richard, Fundamentals of the Theory of Operator Algebras, Vol. II : Advanced Theory, American Mathematical Society. {{ISBN|978-0821808207}}.
• {{citation

• Phoenecia
• Phoenetia Browne
• Phoenicaulis cheiranthoides
• Phoenice Libanensis
• Phoenice Paralia
• Phoenice Prima
• Phoenice (Roman province)
• Phoenicia
• Phoenicia dessert
• Phoenicia International Festival of the Voice
• Phoenicia International Festival of The Voice
• Phoenician
• Phoenician Baalbek
• Phoenician colonization
• Phoenician discovery of America
• Phoenician juniper
• Phoenician people
• Phoenician port in Beirut
• Phoenician port of Beirut
• Phoenician purple
• Phoenician (script)
• Phoenician stadium
• Phoenician (Unicode block)
• Phoenicia (weekly)
• Phoeniciloricus