n!的质因数分解n!de ziyinshu fenjie
为了把n!分解成质因数的连乘积,需要下面几个结果:
❶ 设a,b是两个正整数,则不大于a且为b的倍数的正整数的个数为 [a/b].
证 当a
❷ 设,是素数,若pa|n,但pa+1 |n,则称pa恰好整除n,记作pa|| n.若p是素数,n是正整数,p≤n,则在1,2,…,n中能被pa恰好整除的正整数个数是
|n,则称pa恰好整除n,记作pa|| n.若p是素数,n是正整数,p≤n,则在1,2,…,n中能被pa恰好整除的正整数个数是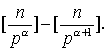
证 由❶知,1,2,…,n中能够被pa整除的正整数个数是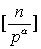 ,能够被p(a+1)整除的正整数个数是
,能够被p(a+1)整除的正整数个数是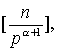 ,因为任一正整数若能被p(a+1)整除,则它一定能被p a整除,于是能被pa恰好整除的正整数个数是
,因为任一正整数若能被p(a+1)整除,则它一定能被p a整除,于是能被pa恰好整除的正整数个数是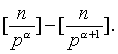
❸ 设在n!的标准分解式中质因数p (p≤n)的方幂指数是h_p,则
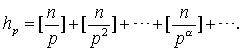
注意,若pa>n,则[n/pa]=0.故上式中只有有限项。设项数为s,则s适合不等式Ps≤n
(s+1),于是
上述结果的证明:我们把正整数1,2,…,n分成若干类,不能被p整除的归入一类,记作N0,能被pa恰好整除的各归入一类,记作Na (a≥1)。由
❷知,在1,2,…,n中能够被pa恰好整除的数的个数是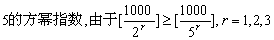 ,因此属于Na类的所有正整数的乘积恰好被pt整除,这里t=
,因此属于Na类的所有正整数的乘积恰好被pt整除,这里t=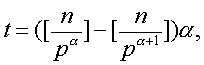 于是
于是
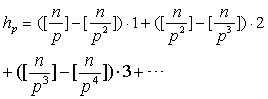
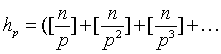 得证。
得证。由这个结果可以推出,
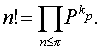 其中
其中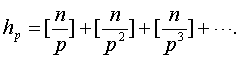 Ⅱ表示连乘积,p≤n表示p通过不超过n的一切质数。
Ⅱ表示连乘积,p≤n表示p通过不超过n的一切质数。例如,求50!的标准分解式中质因数3的方幂指数。
因为
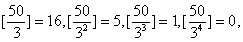 16+5+1=22,因此所求的指数是22。
16+5+1=22,因此所求的指数是22。又例如,求1000!的十进展开式中,末尾有多少个零?这只须看一看在1000!中含10的方幂指数是多少。但10不是素数,因此不能直接利用上述结果。考察2和5的方幂指数,由于
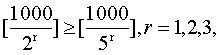 r…1,2,3,…,故在1000!中5的方幂指数不超过2的方幂指数,1000!中末尾含数字零的个数,也就是含5的方幂指数。因为
r…1,2,3,…,故在1000!中5的方幂指数不超过2的方幂指数,1000!中末尾含数字零的个数,也就是含5的方幂指数。因为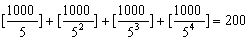 +40+8+1=249。这表明1000!的末尾含有249个零。
+40+8+1=249。这表明1000!的末尾含有249个零。- Jefferies,Richard
- Jefferson City
- Jefferson,Joseph
- Jefferson,Memorial
- Jefferson,Thomas
- Jeffers,Robinson
- Jeffreys of Wem
- Jeffreys,SirHarold
- Jeffrey,Francis,Lord
- Jeffries,John
- jehad
- Jehannet
- Jehoshaphat
- Jehovah′s witnesses
- Jehoyah
- Jehu
- JellicoeJohn Rushwortl Jellicoe.lst Earl
- jellyfish
- Jena
- Jena and Auerstadt,Battle of
- Jenghiz Khan
- Jenkins′Ear,War of
- Jenkins,Roy Harris
- Jenner,Edward
- Jenson,Johannes Vichelm