“Web (differential geometry)”的意思、由来-开放百科全书

词条

Web (differential geometry)

释义

Formal definition
Alternative definition
Remark
Differential geometry of webs
Classical definition
See also
Notes
References

In mathematics, a web permits an intrinsic characterization in terms of Riemannian geometry of the additive separation of variables in the Hamilton–Jacobi equation.^[1]^[2]

Formal definition

An orthogonal web on a Riemannian manifold (M,g) is a set 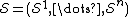of n pairwise transversal and orthogonal foliations of connected submanifolds of codimension 1 and where n denotes the dimension of M.

Note that two submanifolds of codimension 1 are orthogonal if their normal vectors are orthogonal and in a nondefinite metric orthogonality does not imply transversality.

Alternative definition

Given a smooth manifold of dimension n, an orthogonal web (also called orthogonal grid or Ricci’s grid) on a Riemannian manifold (M,g) is a set^[3] 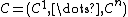of n pairwise transversal and orthogonal foliations of connected submanifolds of dimension 1.

Remark

Since vector fields can be visualized as stream-lines of a stationary flow or as Faraday’s lines of force, a non-vanishing vector field in space generates a space-filling system of lines through each point, known to mathematicians as a congruence (i.e., a local foliation). Ricci’s vision filled Riemann’s n-dimensional manifold with n congruences orthogonal to each other, i.e., a local orthogonal grid.

Differential geometry of webs

A systematic study of webs was started by Blaschke in the 1930s. He extended the same group-theoretic approach to web geometry.

Classical definition

Let 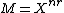be a differentiable manifold of dimension N=nr. A d-web W(d,n,r) of codimension r in an open set 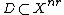is a set of d foliations of codimension r which are in general position.

In the notation W(d,n,r) the number d is the number of foliations forming a web, r is the web codimension, and n is the ratio of the dimension nr of the manifold M and the web codimension. Of course, one may define a d-web of codimension r without having r as a divisor of the dimension of the ambient manifold.

Notes

1. ^{{cite journal|title=Intrinsic characterization of the variable separation in the Hamilton-Jacobi equation |author=S. Benenti|journal=J. Math. Phys. |volume=38|year=1997|pages=6578–6602|issue=12|doi=10.1063/1.532226}}
2. ^{{cite journal | title= Eigenvalues of Killing Tensors and Separable Webs on Riemannian and Pseudo-Riemannian Manifolds | last1 = Chanu | first1= Claudia | last2 = Rastelli|first2 = Giovanni|journal=SIGMA|volume=3 |year=2007|pages=021, 21 pages|doi=10.3842/sigma.2007.021}}
3. ^{{cite journal|authorlink=Gregorio Ricci-Curbastro|title=Dei sistemi di congruenze ortogonali in una varietà qualunque|author=G. Ricci-Curbastro|journal=Mem. Acc. Lincei |volume=2|year=1896|pages=276–322|issue=5}}

References

{{cite book | last = Sharpe | first = R. W. | title = Differential Geometry: Cartan's Generalization of Klein's Erlangen Program | publisher = Springer | location = New York | year=1997 | isbn=0-387-94732-9}}
{{cite book |last1= Dillen |first1= F.J.E.| last2 = Verstraelen | first2 = L.C.A. | title = Handbook of Differential Geometry | publisher = North-Holland | location = Amsterdam | year=2000 |volume=Volume 1 | isbn=0-444-82240-2}}

2 : Differential geometry|Manifolds

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。