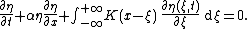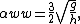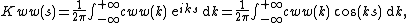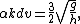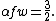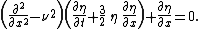“Whitham equation”的意思、由来-开放百科全书

词条

Whitham equation

释义

Water waves
Notes and references
Notes References

{{short description|A non-local model for non-linear dispersive waves}}

In mathematical physics, the Whitham equation is a non-local model for non-linear dispersive waves. ^[1]^[2]^[3]

The equation is notated as follows :

This integro-differential equation for the oscillatory variable η(x,t) is named after Gerald Whitham who introduced it as a model to study breaking of non-linear dispersive water waves in 1967.^[4] Wave breaking – bounded solutions with unbounded derivatives – for the Whitham equation has recently been proven.^[5]

For a certain choice of the kernel K(x − ξ) it becomes the Fornberg–Whitham equation.

Water waves

Using the Fourier transform (and its inverse), with respect to the space coordinate x and in terms of the wavenumber k:

For surface gravity waves, the phase speed c(k) as a function of wavenumber k is taken as:^[4]

{{pad|2em}} while {{pad|2em}}

with g the gravitational acceleration and h the mean water depth. The associated kernel K_ww(s) is, using the inverse Fourier transform:^[4]

since c_ww is an even function of the wavenumber k.

The Korteweg–de Vries equation (KdV equation) emerges when retaining the first two terms of a series expansion of c_ww(k) for long waves with {{nowrap|kh ≪ 1}}:^[4]

{{pad|3em}} {{pad|3em}}

with δ(s) the Dirac delta function.

Bengt Fornberg and Gerald Whitham studied the kernel K_fw(s) – non-dimensionalised using g and h:^[6]

{{pad|2em}} and {{pad|2em}} {{pad|2em}} with {{pad|2em}}

The resulting integro-differential equation can be reduced to the partial differential equation known as the Fornberg–Whitham equation:^[6]

This equation is shown to allow for peakon solutions – as a model for waves of limiting height – as well as the occurrence of wave breaking (shock waves, absent in e.g. solutions of the Korteweg–de Vries equation).^[6]^[3]

Notes and references

Notes

1. ^{{harvtxt|Debnath|2005|p=364}}
2. ^{{harvtxt|Naumkin|Shishmarev|1994|p=1}}
3. ^¹{{harvtxt|Whitham|1974|pp=476–482}}
4. ^¹²³{{harvtxt|Whitham|1967}}
5. ^{{harvtxt|Hur|2017}}
6. ^¹²{{harvtxt|Fornberg|Whitham|1978}}

References

{{Citation

| publisher = Springer
| isbn = 9780817643232
| last = Debnath
| first = L.
| title = Nonlinear Partial Differential Equations for Scientists and Engineers
| year = 2005
}}

{{Citation

| last1 = Fetecau
| first1 = R.
| last2 = Levy
| first2 = Doron
| journal = Communications in Mathematical Sciences
| issue = 2
| pages = 159–170
| title = Approximate Model Equations for Water Waves
| volume = 3
| year = 2005
| doi = 10.4310/CMS.2005.v3.n2.a4
}}

{{Citation

| doi = 10.1098/rsta.1978.0064
| volume = 289
| issue = 1361
| pages = 373–404
| last1 = Fornberg
| first1 = B.
| first2 = G.B.
| last2 = Whitham
| author2-link = Gerald B. Whitham
| title = A Numerical and Theoretical Study of Certain Nonlinear Wave Phenomena
| journal = Philosophical Transactions of the Royal Society A
| year = 1978
|bibcode = 1978RSPTA.289..373F | citeseerx = 10.1.1.67.6331
}}

{{Citation

| last = Hur
| first = V.M.
| title = Wave breaking in the Whitham equation
| journal = Advances in Mathematics
| volume = 317
| pages = 410–437
| year = 2017
| doi = 10.1016/j.aim.2017.07.006
}}

{{Citation

| title = The Whitham Equation as a model for surface water waves
| journal = Physica D: Nonlinear Phenomena
| volume = 309
| pages = 99–107
| year = 2015
| doi = 10.1016/j.physd.2015.07.010
| first1 = D.
| last1 = Moldabayev
| first2 = H.
| last2 = Kalisch
| first3 = D.
| last3 = Dutykh
| arxiv = 1410.8299
| bibcode = 2015PhyD..309...99M
}}

{{Citation

| publisher = American Mathematical Society
| isbn = 9780821845738
| last1 = Naumkin
| first1 = P.I.
| first2 = I.A.
| last2 = Shishmarev
| title = Nonlinear Nonlocal Equations in the Theory of Waves
| year = 1994
}}

{{Citation

| doi = 10.1098/rspa.1967.0119
| volume = 299
| issue = 1456
| pages = 6–25
| last = Whitham
| first = G.B.
| author-link = Gerald B. Whitham
| title = Variational methods and applications to water waves
| journal = Proceedings of the Royal Society A
| year = 1967
|bibcode = 1967RSPSA.299....6W }}

{{Citation

| first = G.B.
| last = Whitham
| author-link = Gerald B. Whitham
| year = 1974
| title = Linear and nonlinear waves
| publisher = Wiley-Interscience
| isbn = 978-0-471-94090-6
| doi=10.1002/9781118032954
}}{{ref end}}

3 : Water waves|Partial differential equations|Equations of fluid dynamics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。