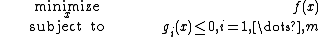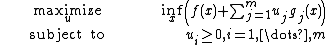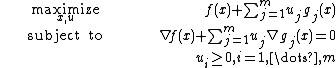- Mathematical formulation
- See also
- References
In mathematical optimization, Wolfe duality, named after Philip Wolfe, is type of dual problem in which the objective function and constraints are all differentiable functions. Using this concept a lower bound for a minimization problem can be found because of the weak duality principle.[1]
Mathematical formulation
For a minimization problem with inequality constraints,
the Lagrangian dual problem is
where the objective function is the Lagrange dual function. Provided that the functions 
and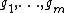 
are convex and continuously differentiable, the infimum occurs where the gradient is equal to zero. The problem
is called the Wolfe dual problem.[2] This problem employs the KKT conditions as a constraint. Also, the equality constraint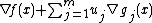 
is nonlinear in general, so the Wolfe dual problem may be a nonconvex optimization problem. In any case, weak duality holds.[3]
See also
- Lagrangian duality
- Fenchel duality
References
2. ^{{cite web|title=Chapter 3. Duality in convex optimization|date=October 30, 2011|url=http://wwwhome.math.utwente.nl/~stillgj/conopt/chap3.pdf|format=pdf|accessdate=May 20, 2012}}
3. ^{{cite journal |last1=Geoffrion |first1=Arthur M. |title=Duality in Nonlinear Programming: A Simplified Applications-Oriented Development | jstor=2028848 |journal=SIAM Review |volume=13 |year=1971 |pages=1–37 |issue=1 |doi=10.1137/1013001}}
- Sumeet Saigal
- Sumeg Castle
- Sumehr
- Sumehsara
- Sumeida's Song
- Su mejor alumno
- Sumenep (city)
- Sumera
- Sumera Hydroelectric Power Plant
- Sumerbank Branch
- Sumerbank Shuttle Railway
- Sumer, Bhopal
- Sumer, Bulgaria
- Sumer (disambiguation)
- Sumerduck Historic District
- Sumeria
- Sumeria(disambiguation)
- Sumerian
- Sumerian debates
- Sumerian disputations
- Sumerian flood
- Sumerian Kyngs
- Sumerian mythos
- Sumerian paradise
- Sumerians