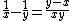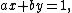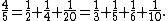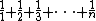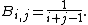“Unit fraction”的意思、由来-开放百科全书

A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n. Examples are 1/1, 1/2, 1/3, 1/4 ,1/5, etc.

Elementary arithmetic

Multiplying any two unit fractions results in a product that is another unit fraction:

However, adding, subtracting, or dividing two unit fractions produces a result that is generally not a unit fraction:

Modular arithmetic

Unit fractions play an important role in modular arithmetic, as they may be used to reduce modular division to the calculation of greatest common divisors. Specifically, suppose that we wish to perform divisions by a value x, modulo y. In order for division by x to be well defined modulo y, x and y must be relatively prime. Then, by using the extended Euclidean algorithm for greatest common divisors we may find a and b such that

Finite sums of unit fractions

Any positive rational number can be written as the sum of unit fractions, in multiple ways. For example,

The ancient Egyptian civilisations used sums of distinct unit fractions in their notation for more general rational numbers, and so such sums are often called Egyptian fractions. There is still interest today in analyzing the methods used by the ancients to choose among the possible representations for a fractional number, and to calculate with such representations.^[1] The topic of Egyptian fractions has also seen interest in modern number theory; for instance, the Erdős–Graham conjecture and the Erdős–Straus conjecture concern sums of unit fractions, as does the definition of Ore's harmonic numbers.

In geometric group theory, triangle groups are classified into Euclidean, spherical, and hyperbolic cases according to whether an associated sum of unit fractions is equal to one, greater than one, or less than one respectively.

Series of unit fractions

Many well-known infinite series have terms that are unit fractions. These include:

Matrices of unit fractions

It has the unusual property that all elements in its inverse matrix are integers.^[2] Similarly, {{harvtxt|Richardson|2001}} defined a matrix with elements

where F_i denotes the ith Fibonacci number. He calls this matrix the Filbert matrix and it has the same property of having an integer inverse.^[3]

Adjacent fractions

Two fractions are called adjacent if their difference is a unit fraction.^[4]^[5]

Unit fractions in probability and statistics

In a uniform distribution on a discrete space, all probabilities are equal unit fractions. Due to the principle of indifference, probabilities of this form arise frequently in statistical calculations.^[6] Additionally, Zipf's law states that, for many observed phenomena involving the selection of items from an ordered sequence, the probability that the nth item is selected is proportional to the unit fraction 1/n.^[7]

Unit fractions in physics

The energy levels of photons that can be absorbed or emitted by a hydrogen atom are, according to the Rydberg formula, proportional to the differences of two unit fractions. An explanation for this phenomenon is provided by the Bohr model, according to which the energy levels of electron orbitals in a hydrogen atom are inversely proportional to square unit fractions, and the energy of a photon is quantized to the difference between two levels.^[8]

See also

References

1. ^{{citation | last = Guy | first = Richard K. | author-link = Richard K. Guy | contribution = D11. Egyptian Fractions | edition = 3rd | isbn = 978-0-387-20860-2 | pages = 252–262 | publisher = Springer-Verlag | title = Unsolved problems in number theory | year = 2004}}.
2. ^{{citation | last = Choi | first = Man Duen | doi = 10.2307/2975779 | mr = 701570 | issue = 5 | journal = The American Mathematical Monthly | pages = 301–312 | title = Tricks or treats with the Hilbert matrix | volume = 90 | year = 1983}}.
3. ^{{citation | last = Richardson | first = Thomas M. | title = The Filbert matrix | journal = Fibonacci Quarterly | volume = 39 | issue = 3 | year = 2001 | pages = 268–275 | arxiv = math.RA/9905079 | bibcode = 1999math......5079R | url = http://www.fq.math.ca/Scanned/39-3/richardson.pdf}}
4. ^{{PlanetMath|urlname=AdjacentFraction|title=Adjacent Fraction}}
5. ^{{MathWorld |title=Adjacent Fraction |id=AdjacentFraction}}
6. ^{{citation|page=66|title=Aspects of statistical inference|volume=246|series=Wiley Series in Probability and Statistics|first=Alan H.|last=Welsh|publisher=John Wiley and Sons|year=1996|isbn=978-0-471-11591-5}}.
7. ^{{citation|title=Theory of Zipf's Law and Beyond|volume=632|series=Lecture Notes in Economics and Mathematical Systems|first1=Alexander|last1=Saichev|first2=Yannick|last2=Malevergne|first3=Didier|last3=Sornette|publisher=Springer-Verlag|year=2009|isbn=978-3-642-02945-5}}.
8. ^{{citation|pages=81–86|title=Modern Atomic and Nuclear Physics|first1=Fujia|last1=Yang|first2=Joseph H.|last2=Hamilton|publisher=World Scientific|year=2009|isbn=978-981-283-678-6}}.
9. ^{{citation|title=Eddington's search for a fundamental theory: a key to the universe|first=Clive William|last=Kilmister|publisher=Cambridge University Press|year=1994|isbn=978-0-521-37165-0}}.