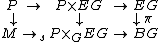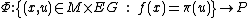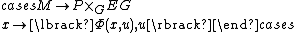“Universal bundle”的意思、由来-开放百科全书

词条

Universal bundle

释义

Existence of a universal bundle
In the CW complex category For compact Lie groups
Use in the study of group actions
Examples
See also
External links
Notes

In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group {{mvar|G}}, is a specific bundle over a classifying space {{mvar|BG}}, such that every bundle with the given structure group {{mvar|G}} over {{mvar|M}} is a pullback by means of a continuous map {{math|M → BG}}.

Existence of a universal bundle

In the CW complex category

When the definition of the classifying space takes place within the homotopy category of CW complexes, existence theorems for universal bundles arise from Brown's representability theorem.

For compact Lie groups

We will first prove:

Proposition. Let {{mvar|G}} be a compact Lie group. There exists a contractible space {{mvar|EG}} on which {{mvar|G}} acts freely. The projection {{math|EG → BG}} is a {{mvar|G}}-principal fibre bundle.

Proof. There exists an injection of {{mvar|G}} into a unitary group {{math|U(n)}} for {{mvar|n}} big enough.^[1] If we find {{math|EU(n)}} then we can take {{mvar|EG}} to be {{math|EU(n)}}. The construction of {{math|EU(n)}} is given in classifying space for {{math|U(n)}}.

The following Theorem is a corollary of the above Proposition.

Theorem. If {{mvar|M}} is a paracompact manifold and {{math|P → M}} is a principal {{mvar|G}}-bundle, then there exists a map {{math| f : M → BG}}, unique up to homotopy, such that {{mvar|P}} is isomorphic to {{math| f ^∗(EG)}}, the pull-back of the {{mvar|G}}-bundle {{math|EG → BG}} by {{math| f}}.

Proof. On one hand, the pull-back of the bundle {{math|π : EG → BG}} by the natural projection {{math|P ×_G EG → BG}} is the bundle {{math|P × EG}}. On the other hand, the pull-back of the principal {{mvar|G}}-bundle {{math|P → M}} by the projection {{math|p : P ×_G EG → M}} is also {{math|P × EG}}

Since {{mvar|p}} is a fibration with contractible fibre {{mvar|EG}}, sections of {{mvar|p}} exist.^[2] To such a section {{mvar|s}} we associate the composition with the projection {{math|P ×_G EG → BG}}. The map we get is the {{math| f }} we were looking for.

For the uniqueness up to homotopy, notice that there exists a one-to-one correspondence between maps {{math| f : M → BG}} such that {{math| f ^∗(EG) → M}} is isomorphic to {{math|P → M}} and sections of {{mvar|p}}. We have just seen how to associate a {{math| f }} to a section. Inversely, assume that {{math| f }} is given. Let {{math|Φ : f ^∗(EG) → P}} be an isomorphism:

Now, simply define a section by

Because all sections of {{mvar|p}} are homotopic, the homotopy class of {{math| f }} is unique.

Use in the study of group actions

The total space of a universal bundle is usually written {{mvar|EG}}. These spaces are of interest in their own right, despite typically being contractible. For example, in defining the homotopy quotient or homotopy orbit space of a group action of {{mvar|G}}, in cases where the orbit space is pathological (in the sense of being a non-Hausdorff space, for example). The idea, if {{mvar|G}} acts on the space {{mvar|X}}, is to consider instead the action on {{math|Y {{=}} X × EG}}, and corresponding quotient. See equivariant cohomology for more detailed discussion.

If {{mvar|EG}} is contractible then {{mvar|X}} and {{mvar|Y}} are homotopy equivalent spaces. But the diagonal action on {{mvar|Y}}, i.e. where {{mvar|G}} acts on both {{mvar|X}} and {{mvar|EG}} coordinates, may be well-behaved when the action on {{mvar|X}} is not.

Examples

Classifying space for U(n)

External links

PlanetMath page of universal bundle examples

Notes

1. ^J. J. Duistermaat and J. A. Kolk,-- Lie Groups, Universitext, Springer. Corollary 4.6.5
2. ^A.~Dold -- Partitions of Unity in the Theory of Fibrations, Annals of Mathematics, vol. 78, No 2 (1963)

2 : Homotopy theory|Fiber bundles

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。