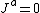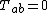- Examples Maxwell's equations Einstein field equations Black hole vacuum solution Kasner space Kaluza–Klein theory
- See also
- Notes
- References
}}
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction (i.e.- set to zero).
Examples
Maxwell's equations
{{main|Maxwell's equations}}In Maxwell's theory of electromagnetism, a vacuum solution would represent the electromagnetic field in a region of space where there are no electromagnetic sources (charges and electric currents), i.e. where the current{{clarify|why is the current vector singled out?|date=December 2016}} 4-vector vanishes:[1]
Einstein field equations
{{main|Einstein field equations|Vacuum solution (general relativity)}}In Einstein's theory of general relativity, a vacuum solution[2] would represent the gravitational field in a region of spacetime where there are no gravitational sources (masses), i.e. where the energy–momentum tensor vanishes:[3]
Black hole vacuum solution
{{main|Kerr metric}}{{expand section|date=December 2016}}Kasner space
{{main|Kasner metric}}Kasner vacuum solution[4]
{{expand section|date=December 2016}}Kaluza–Klein theory
{{main|Kaluza–Klein theory}}In a Kaluza–Klein vacuum (static) field equations[5]
See also
- Vacuum solution (general relativity)
- Topological defect
Notes
1. ^{{Citation | doi = 10.1016/S0375-9601(96)00872-9 | title = Classical vgr? c solutions of Maxwell's equations and the photon tunneling effect | url = http://linkinghub.elsevier.com/retrieve/pii/S0375960196008729 | year = 1997 | author = Esposito, S. | journal = Physics Letters A | pages = 203–209 | volume = 225 | issue = 4-6 | accessdate = 2009-07-04|arxiv = physics/9611018 |bibcode = 1997PhLA..225..203E }}
2. ^{{Citation | title = Exact solutions of Einstein's field equations | url = https://www.loc.gov/catdir/samples/cam033/2002071495.pdf | year = 2003 | author = Stephani, H. | accessdate = 2009-07-04}}
3. ^{{Citation | doi = 10.1002/prop.2190381002 | title = Multipole Moments in General Relativity-Static and Stationary Vacuum Solutions | url = http://www3.interscience.wiley.com/journal/112587363/abstract | archive-url = https://archive.today/20130105092100/http://www3.interscience.wiley.com/journal/112587363/abstract | dead-url = yes | archive-date = 2013-01-05 | year = 1990 | author = Quevedo, H. | pages = 733 | journal = Fortschritte der Physik | volume = 38 | issue = 10 | accessdate = 2009-07-04|bibcode = 1990ForPh..38..733Q }}
4. ^{{Citation | title = Where has the fifth dimension gone? | doi = 10.1103/PhysRevD.21.2167 | year = 1980 | journal = Physical Review D | pages = 2167–2170 | volume = 21 | issue = 8 | last1 = Chodos | first1 = A. | last2 = Detweiler | first2 = S. |bibcode = 1980PhRvD..21.2167C }}
5. ^{{Citation | title = Kaluza-klein monopole | doi = 10.1103/PhysRevLett.51.87 | year = 1983 | author = Sorkin, R.D. | journal = Physical Review Letters | pages = 87–90 | volume = 51 | issue = 2| bibcode=1983PhRvL..51...87S}}
2. ^{{Citation | title = Exact solutions of Einstein's field equations | url = https://www.loc.gov/catdir/samples/cam033/2002071495.pdf | year = 2003 | author = Stephani, H. | accessdate = 2009-07-04}}
3. ^{{Citation | doi = 10.1002/prop.2190381002 | title = Multipole Moments in General Relativity-Static and Stationary Vacuum Solutions | url = http://www3.interscience.wiley.com/journal/112587363/abstract | archive-url = https://archive.today/20130105092100/http://www3.interscience.wiley.com/journal/112587363/abstract | dead-url = yes | archive-date = 2013-01-05 | year = 1990 | author = Quevedo, H. | pages = 733 | journal = Fortschritte der Physik | volume = 38 | issue = 10 | accessdate = 2009-07-04|bibcode = 1990ForPh..38..733Q }}
4. ^{{Citation | title = Where has the fifth dimension gone? | doi = 10.1103/PhysRevD.21.2167 | year = 1980 | journal = Physical Review D | pages = 2167–2170 | volume = 21 | issue = 8 | last1 = Chodos | first1 = A. | last2 = Detweiler | first2 = S. |bibcode = 1980PhRvD..21.2167C }}
5. ^{{Citation | title = Kaluza-klein monopole | doi = 10.1103/PhysRevLett.51.87 | year = 1983 | author = Sorkin, R.D. | journal = Physical Review Letters | pages = 87–90 | volume = 51 | issue = 2| bibcode=1983PhRvL..51...87S}}
References
- {{Citation
| title = Gravitational lensing effects of vacuum strings- Exact solutions
| bibcode = 1985ApJ...288..422G
| year = 1985
| journal = Astrophysical Journal
| volume = 288
| issue = Part 1
| last1 = Gott | first1 = J.R.
| last2 = Richard | first2 = J. |doi = 10.1086/162808 }}
- {{Citation
| doi = 10.1007/s002200050571
| title = The initial boundary value problem for Einstein's vacuum field equation
| url = http://math.msu.edu/~gnagy/papers/hFgN99.pdf
| year = 1999
| journal = Communications in Mathematical Physics
| pages = 619–655
| volume = 201
| issue = 3
| last1 = Friedrich | first1 = H.
| last2 = Nagy | first2 = G.
| accessdate = 2009-07-04 |bibcode = 1999CMaPh.201..619F }}
- {{Citation
| title = Quantum dynamics of Kaluza-Klein theories
| doi = 10.1103/PhysRevD.28.772
| year = 1983
| journal = Physical Review D
| pages = 772–784
| volume = 28
| issue = 4
| last1 = Appelquist | first1 = T.
| last2 = Chodos | first2 = A. |bibcode = 1983PhRvD..28..772A }}
1 : Theoretical physics
- Oh Taeseok
- Ohtahara Syndrome
- Ohta Jidosha
- Ohtakari
- Oh Takbeon
- Oh Tak-bon
- Ohtake
- Ohtanajärvi/Aapua FF
- Ohtanajärvi IK
- Ohtani Tomoya
- Ohta publishing
- Ohta Publishing
- Ohta Publishing Company
- Ohta Shuppan
- Ohtemachi
- Oh the Deep, Deep Love of Jesus
- Oh The Grandeur
- Oh the red viburnum in the meadow
- Ohthere's Mound
- Oh The Things Mommies Do! What Could Be Better Than Having Two?
- Oh, This Old Thing?
- Oh, This Old Thing
- Oh Those Bells
- Oh. Those Bells!
- Oh, Those Bells