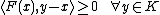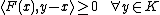- History
- Definition
- Examples The problem of finding the minimal value of a real-valued function of real variable The general finite-dimensional variational inequality The variational inequality for the Signorini problem
- See also
- References Historical references Scientific works
- External links
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all possible values of a given variable, belonging usually to a convex set. The mathematical theory of variational inequalities was initially developed to deal with equilibrium problems, precisely the Signorini problem: in that model problem, the functional involved was obtained as the first variation of the involved potential energy therefore it has a variational origin, recalled by the name of the general abstract problem. The applicability of the theory has since been expanded to include problems from economics, finance, optimization and game theory.
History
The first problem involving a variational inequality was the Signorini problem, posed by Antonio Signorini in 1959 and solved by Gaetano Fichera in 1963, according to the references {{Harv|Antman|1983|pp=282–284}} and {{Harv|Fichera|1995}}: the first papers of the theory were {{Harv|Fichera|1963}} and {{Harv|Fichera|1964a}}, {{Harv|Fichera|1964b}}. Later on, Guido Stampacchia proved his generalization to the Lax–Milgram theorem in {{Harv|Stampacchia|1964}} in order to study the regularity problem for partial differential equations and coined the name "variational inequality" for all the problems involving inequalities of this kind. Georges Duvaut encouraged his graduate students to study and expand on Fichera's work, after attending a conference in Brixen on 1965 where Fichera presented his study of the Signorini problem, as {{Harvnb|Antman|1983|p=283}} reports: thus the theory become widely known throughout France. Also in 1965, Stampacchia and Jacques-Louis Lions extended earlier results of {{Harv|Stampacchia|1964}}, announcing them in the paper {{Harv|Lions|Stampacchia|1965}}: full proofs of their results appeared later in the paper {{Harv|Lions|Stampacchia|1967}}.
Definition
Following {{Harvtxt|Antman|1983|p=283}}, the formal definition of a variational inequality is the following one.
{{EquationRef|1|Definition 1.}} Given a Banach space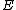 , a subset
, a subset 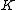 of
of 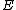 , and a functional
, and a functional 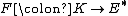 from
from 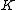 to the dual space
to the dual space 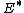 of the space
of the space 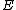 ,
,the variational inequality problem
is the problem of solving
for the variable  belonging to
belonging to 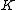 the following inequality:
the following inequality:
where 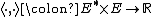
is the duality pairing.
In general, the variational inequality problem can be formulated on any finite – or infinite-dimensional Banach space. The three obvious steps in the study of the problem are the following ones:
- Prove the existence of a solution: this step implies the mathematical correctness of the problem, showing that there is at least a solution.
- Prove the uniqueness of the given solution: this step implies the physical correctness of the problem, showing that the solution can be used to represent a physical phenomenon. It is a particularly important step since most of the problems modeled by variational inequalities are of physical origin.
- Find the solution.
Examples
The problem of finding the minimal value of a real-valued function of real variable
This is a standard example problem, reported by {{Harvtxt|Antman|1983|p=283}}: consider the problem of finding the minimal value of a differentiable function  over a closed interval
over a closed interval 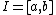 . Let
. Let 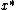 be a point in
be a point in  where the minimum occurs. Three cases can occur:
where the minimum occurs. Three cases can occur:
- if
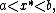 then
then 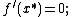
- if
 then
then 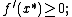
- if
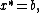 then
then 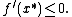
These necessary conditions can be summarized as the problem of finding 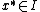 such that
such that
for
The absolute minimum must be searched between the solutions (if more than one) of the preceding inequality: note that the solution is a real number, therefore this is a finite dimensional variational inequality.
The general finite-dimensional variational inequality
A formulation of the general problem in 
is the following: given a subset
 of
of

and a mapping
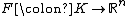 ,
,
the finite-dimensional variational inequality problem associated with 
consist of finding a  -dimensional vector
-dimensional vector  belonging to
belonging to
 such that
such that
where 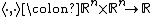
is the standard inner product on the vector space  .
.
The variational inequality for the Signorini problem
In the historical survey {{Harv|Fichera|1995}}, Gaetano Fichera describes the genesis of his solution to the Signorini problem: the problem consist in finding the elastic equilibrium configuration
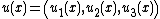
of an anisotropic non-homogeneous elastic body that lies in a subset
 of the three-dimensional euclidean space whose boundary is
of the three-dimensional euclidean space whose boundary is  , resting on a rigid frictionless surface and subject only to its mass forces.
, resting on a rigid frictionless surface and subject only to its mass forces.
The solution  of the problem exists and is unique (under precise assumptions) in the set of admissible displacements
of the problem exists and is unique (under precise assumptions) in the set of admissible displacements

i.e. the set of displacement vectors satisfying the system of ambiguous boundary conditions if and only if
where 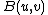
and 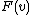
are the following functionals,
written using the Einstein notation
,
,
where, for all 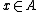 ,
,
 is the contact surface (or more generally a contact set),
is the contact surface (or more generally a contact set),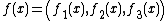 is the body force applied to the body,
is the body force applied to the body,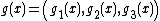 is the surface force applied to
is the surface force applied to  ,
,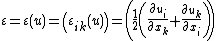 is the infinitesimal strain tensor,
is the infinitesimal strain tensor,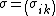 is the Cauchy stress tensor, defined as
is the Cauchy stress tensor, defined as
whereis the elastic potential energy and
is the elasticity tensor.
See also
- Complementarity theory
- Differential variational inequality
- Extended Mathematical Programming for Equilibrium Problems
- Mathematical programming with equilibrium constraints
- Obstacle problem
- Projected dynamical system
- Signorini problem
References
Historical references
- {{Citation
| last = Antman
| first = Stuart
| authorlink = Stuart Antman
| author-link =
| title = The influence of elasticity in analysis: modern developments
| journal = Bulletin of the American Mathematical Society
| volume = 9
| issue = 3
| pages = 267–291
| date =
| year = 1983
| url = http://www.ams.org/bull/1983-09-03/S0273-0979-1983-15185-6/home.html
| doi = 10.1090/S0273-0979-1983-15185-6
| mr = 714990
| zbl = 0533.73001
}}. An historical paper about the fruitful interaction of elasticity theory and mathematical analysis: the creation of the theory of variational inequalities by Gaetano Fichera is described in §5, pages 282–284.
- {{Citation
| last = Duvaut
| first = Georges
| author-link =Georges Duvaut
| contribution = Problèmes unilatéraux en mécanique des milieux continus
| contribution-url = http://www.mathunion.org/ICM/ICM1970.3/Main/icm1970.3.0071.0078.ocr.pdf
| series = ICM Proceedings
| title = Actes du Congrès international des mathématiciens, 1970
| volume = Mathématiques appliquées (E), Histoire et Enseignement (F) – Volume 3
| pages = 71–78
| year = 1971
| place = Paris
| publisher = Gauthier-Villars
| url = http://www.mathunion.org/ICM/ICM1970.3/
| id =
| mr =
| zbl =
}}. A brief research survey describing the field of variational inequalities, precisely the sub-field of continuum mechanics problems with unilateral constraints.
- {{Citation
| first = Gaetano
| last = Fichera
| author-link = Gaetano Fichera
| editor-last =
| editor-first =
| contribution = La nascita della teoria delle disequazioni variazionali ricordata dopo trent'anni
| title = Incontro scientifico italo-spagnolo. Roma, 21 ottobre 1993
| url = http://www.lincei.it/pubblicazioni/catalogo/volume.php?lg=e&rid=32885
| language = Italian
| year = 1995
| pages = 47–53
| place = Roma
| series = Atti dei Convegni Lincei
| volume = 114
| publisher = Accademia Nazionale dei Lincei
}}. The birth of the theory of variational inequalities remembered thirty years later (English translation of the title) is an historical paper describing the beginning of the theory of variational inequalities from the point of view of its founder.
Scientific works
- {{Citation
| last1=Facchinei
| first1=Francisco
| author1-link=
| last2=Pang
| first2=Jong-Shi
| author2-link=
| title=Finite Dimensional Variational Inequalities and Complementarity Problems, Vol. 1
| series = Springer Series in Operations Research
| publisher=Springer-Verlag
| location= Berlin–Heidelberg–New York
| isbn=0-387-95580-1
| year=2003
| zbl=1062.90001
}}
- {{Citation
| last1=Facchinei
| first1=Francisco
| author1-link=
| last2=Pang
| first2=Jong-Shi
| author2-link=
| title=Finite Dimensional Variational Inequalities and Complementarity Problems, Vol. 2
| series = Springer Series in Operations Research
| publisher=Springer-Verlag
| location= Berlin–Heidelberg–New York
| isbn=0-387-95581-X
| year=2003
| zbl=1062.90001
}}
- {{citation
| last = Fichera
| first = Gaetano
| author-link = Gaetano Fichera
| title = Sul problema elastostatico di Signorini con ambigue condizioni al contorno
| journal = Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali
| language = Italian
| volume = 34
| series = 8
| issue = 2
| year = 1963
| pages=138–142
| zbl= 0128.18305
}}. "On the elastostatic problem of Signorini with ambiguous boundary conditions" (English translation of the title) is a short research note announcing and describing the solution of the Signorini problem.
- {{citation
| last = Fichera
| first = Gaetano
| author-link = Gaetano Fichera
| title = Problemi elastostatici con vincoli unilaterali: il problema di Signorini con ambigue condizioni al contorno
| journal = Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali
| language = Italian
| volume = 7
| series = 8
| issue = 2
| year = 1964a
| pages=91–140
| zbl = 0146.21204
}}. "Elastostatic problems with unilateral constraints: the Signorini problem with ambiguous boundary conditions" (English translation of the title) is the first paper where an existence and uniqueness theorem for the Signorini problem is proved.
- {{citation
| last = Fichera
| first = Gaetano
| contribution = Elastostatic problems with unilateral constraints: the Signorini problem with ambiguous boundary conditions
| title = Seminari dell'istituto Nazionale di Alta Matematica 1962–1963
| year = 1964b
| publisher = Edizioni Cremonese
| place = Rome
| pages=613–679
}}. An English translation of {{Harv|Fichera|1964a}}.
- {{Citation
| last = Glowinski
| first = Roland
| author-link = Roland Glowinski
| last2 = Lions
| first2 = Jacques-Louis
| author2-link = Jacques-Louis Lions
| last3 = Trémolières
| first3 = Raymond
| author3-link=
| title = Numerical analysis of variational inequalities. Translated from the French
| place = Amsterdam–New York–Oxford
| publisher = North-Holland
| year = 1981
| series = Studies in Mathematics and its Applications
| volume = 8
| mr = 635927
| isbn = 0-444-86199-8
| zbl = 0463.65046
| pages = xxix+776 }}
- {{Citation
| last1=Kinderlehrer
| first1=David
| author1-link=David Kinderlehrer
| last2=Stampacchia
| first2=Guido
| author2-link=Guido Stampacchia
| title=An Introduction to Variational Inequalities and Their Applications
| publisher=Academic Press
| series= Pure and Applied Mathematics
| url = https://books.google.com/books?id=B1cPRJ3qiw0C&printsec=frontcover&dq=An+Introduction+to+Variational+Inequalities+and+Their+Applications
| volume = 88
| location=Boston–London–New York–San Diego–Sydney–Tokyo–Toronto
| isbn=0-89871-466-4
| year=1980
| zbl=0457.35001}}.
- {{Citation
| last = Lions
| first = Jacques-Louis
| author-link = Jacques-Louis Lions
| last2 = Stampacchia
| first2 = Guido
| author2-link = Guido Stampacchia
| title = Inéquations variationnelles non coercives
| journal = Comptes rendus hebdomadaires des séances de l'Académie des sciences
| volume = 261
| pages = 25–27
| year = 1965
| url = http://gallica.bnf.fr/ark:/12148/bpt6k4022z.image.r=Comptes+Rendus+Academie.langEN.f26.pagination
| zbl = 0136.11906
}}, available at Gallica. Announcements of the results of paper {{Harv|Lions|Stampacchia|1967}}.
- {{Citation
| last = Lions
| first = Jacques-Louis
| author-link = Jacques-Louis Lions
| last2 = Stampacchia
| first2 = Guido
| author2-link = Guido Stampacchia
| title = Variational inequalities
| journal = [https://archive.today/20130105082552/http://www3.interscience.wiley.com/journal/29240/home?CRETRY=1&SRETRY=0 Communications on Pure and Applied Mathematics]
| volume = 20
| pages = 493–519
| year = 1967
| url = http://www3.interscience.wiley.com/journal/113397217/abstract
| doi = 10.1002/cpa.3160200302
| zbl = 0152.34601
| issue = 3
}}{{dead link|date=February 2019|bot=medic}}{{cbignore|bot=medic}}. An important paper, describing the abstract approach of the authors to the theory of variational inequalities.
- {{citation
|last=Roubíček
|first= Tomáš
|title=Nonlinear Partial Differential Equations with Applications
|series=ISNM. International Series of Numerical Mathematics
|volume=153
|publisher= Birkhäuser Verlag
|place= Basel–Boston–Berlin
|pages= xx+476
|edition=2nd
|year= 2013
|isbn= 978-3-0348-0512-4
|mr=3014456
|zbl=1270.35005
|doi=10.1007/978-3-0348-0513-1}}.
- {{Citation
| last = Stampacchia
| first = Guido
| author-link = Guido Stampacchia
| title = Formes bilineaires coercitives sur les ensembles convexes
| journal = Comptes rendus hebdomadaires des séances de l'Académie des sciences
| volume = 258
| pages = 4413–4416
| year = 1964
| url = http://gallica.bnf.fr/ark:/12148/bpt6k4012p.image.r=Comptes+Rendus+Academie.f20.langEN
| doi =
| zbl = 0124.06401
}}, available at Gallica. The paper containing Stampacchia's generalization of the Lax–Milgram theorem.
External links
- {{springer
| title= Variational inequalities
| id= V/v120010
| last= Panagiotopoulos
| first= P.D.
| author-link=
}}
- [https://www.scilag.net/problem/G-180630.1 Alessio Figalli, On global homogeneous solutions to the Signorini problem,]
- Prince Charles Foreland
- Prince Charles Gustavus Oscar Frederick Christian of Sweden
- Prince Charles Hotel
- Prince Charles John Arthur of Sweden
- Prince Charles (Q-ship)
- Prince Charles stream tree frog
- Prince Charles, the Duke of Rothesay
- Prince Charles, Wales
- Prince Charles William Louis of Sweden
- Prince Charles William of Hesse-Darmstadt
- Prince Charlies Cave
- Prince Charming (1999 film)
- Prince Charming (TV film)
- Prince Chichibu
- Prince Chigi
- Prince Chlodwig of Hohenlohe-Schillingsfurst
- Prince Chonger
- Prince Chong'er
- Prince Christian of Denmark (1675-1695)
- Prince Christian of Denmark (1675–1695)
- Prince Christian of Hanover (b. 1985)
- Prince Christian of Hanover (born 1985)
- Prince Christian of Hesse
- Prince Christian of Hesse-Philippsthal-Barchfeld
- Prince Christian of Schaumburg-Lippe (1974)