- References
- External links
In mathematics, variational perturbation theory (VPT) is a mathematical method to convert divergent power series in a small expansion parameter, say
,
into a convergent series in powers
,
where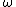 
is a critical exponent (the so-called index of "approach to scaling" introduced by Franz Wegner). This is possible with the help of variational parameters, which are determined by optimization order by order in 
. The partial sums are converted to convergent partial sums by a method developed in 1992.[1]
Most perturbation expansions in quantum mechanics are divergent for any small coupling strength . They can be made convergent by VPT (for details see the first textbook cited below). The convergence is exponentially fast.[2][3]
After its success in quantum mechanics, VPT has been developed further to become an important mathematical tool in quantum field theory with its anomalous dimensions.[4] Applications focus on the theory of critical phenomena. It has led to the most accurate predictions of critical exponents.
More details can be read here.
References
2. ^{{cite journal |last1=Kleinert |first1=H. |author-link=Hagen Kleinert |last2=Janke |first2=W. |year=1993 |title=Convergence Behavior of Variational Perturbation Expansion - A Method for Locating Bender-Wu Singularities |url=http://users.physik.fu-berlin.de/~kleinert/235/235.pdf |journal=Physics Letters A |volume=206 |issue= |pages=283–289 |arxiv=quant-ph/9509005 |bibcode=1995PhLA..206..283K |doi=10.1016/0375-9601(95)00521-4}}
3. ^{{cite journal |last1=Guida |first1=R. |last2=Konishi |first2=K. |last3=Suzuki |first3=H. |year=1996 |title=Systematic Corrections to Variational Calculation of Effective Classical Potential |journal=Annals of Physics |volume=249 |issue=1 |pages=109–145 |arxiv=hep-th/9505084 |bibcode=1996AnPhy.249..109G |doi=10.1006/aphy.1996.0066}}
4. ^{{cite journal |last1=Kleinert |first1=H. |author-link=Hagen Kleinert |year=1998 |title=Strong-coupling behavior of φ^4 theories and critical exponents |url=http://users.physik.fu-berlin.de/~kleinert/257/257.pdf |journal=Physical Review D |volume=57 |issue=4 |page=2264 |bibcode=1998PhRvD..57.2264K |doi=10.1103/PhysRevD.57.2264}}
External links
- Kleinert H., Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3. Auflage, World Scientific (Singapore, 2004) (readable online here) (see Chapter 5)
- Kleinert H. and Verena Schulte-Frohlinde, Critical Properties of φ4-Theories, World Scientific (Singapur, 2001); Paperback {{ISBN|981-02-4658-7}} (readable online here) (see Chapter 19)
- {{cite journal
|last=Feynman|first=R. P.|author1-link=Richard P. Feynman
|last2=Kleinert |first2=H. |author2-link=Hagen Kleinert
|year=1986
|title=Effective classical partition functions
|journal=Physical Review A
|volume=34 |issue=6 |pages=5080–5084
|bibcode=1986PhRvA..34.5080F
|doi=10.1103/PhysRevA.34.5080
|pmid=9897894}}