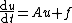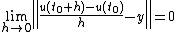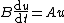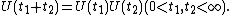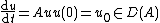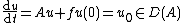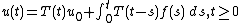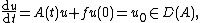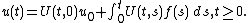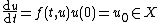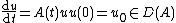- Abstract Cauchy problem Definition Well posedness Semigroup of operators associated to a Cauchy problem
- Nonhomogeneous problem
- Time-dependent problem
- Non linear problem
- See also
- References
In mathematics, an abstract differential equation is a differential equation in which the unknown function and its derivatives take values in some generic abstract space (a Hilbert space, a Banach space, etc.). Equations of this kind arise e.g. in the study of partial differential equations: if to one of the variables is given a privilegiate position (e.g. time, in heat or wave equations) and all the others are put together, an ordinary "differential" equation with respect to the variable which was put in evidence is obtained. Adding boundary conditions can often be translated in terms of considering solutions in some convenient function spaces.
The classical abstract differential equation which is most frequently encountered is the equation[1]
where the unknown function 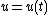 belongs to some function space
belongs to some function space  ,
, 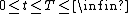 and
and 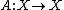 is an operator (usually a linear operator) acting on this space. An exhaustive treatment of the homogeneous (
is an operator (usually a linear operator) acting on this space. An exhaustive treatment of the homogeneous ( ) case with a constant operator is given by the theory of C0-semigroups. Very often, the study of other abstract differential equations amounts (by e.g. reduction to a set of equations of the first order) to the study of this equation.
) case with a constant operator is given by the theory of C0-semigroups. Very often, the study of other abstract differential equations amounts (by e.g. reduction to a set of equations of the first order) to the study of this equation.
The theory of abstract differential equations has been founded by professor Einar Hille in several papers and in his book Functional Analysis and Semi-Groups.[2] Other main contributors were[3] Kōsaku Yosida, Ralph Phillips, Isao Miyadera and Selim Grigorievich Krein.
Abstract Cauchy problem
Definition
Let[4][5][6]  and
and  be two linear operators, with domains
be two linear operators, with domains 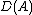 and
and 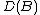 , acting in a Banach space
, acting in a Banach space  . A function
. A function 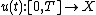 is said to have strong derivative (or to be Frechet differentiable or simply differentiable) at the point
is said to have strong derivative (or to be Frechet differentiable or simply differentiable) at the point  if there exists an element
if there exists an element 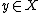 such that
such that
and its derivative is 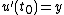 .
.
A solution of the equation
is a function 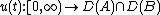 such that:
such that:
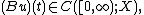
- the strong derivative
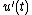 exists
exists 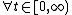 and
and  for any such
for any such  , and
, and - the previous equality holds
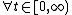 .
.
The Cauchy problem consists in finding a solution of the equation, satisfying the initial condition 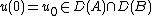 .
.
Well posedness
According to the definition of well-posed problem by Hadamard, the Cauchy problem is said to be well posed (or correct) on  if:
if:
- for any
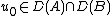 it has a unique solution, and
it has a unique solution, and - this solution depends continuously on the initial data in the sense that if
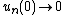 (
(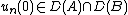 ), then
), then 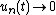 for the corresponding solution at every
for the corresponding solution at every 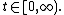
A well posed Cauchy problem is said to be uniformly well posed if 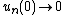 implies
implies 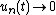 uniformly in
uniformly in  on each finite interval
on each finite interval  .
.
Semigroup of operators associated to a Cauchy problem
To an abstract Cauchy problem one can associate a semigroup of operators  , i.e. a family of bounded linear operators depending on a parameter
, i.e. a family of bounded linear operators depending on a parameter  (
(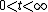 ) such that
) such that
Consider the operator  which assigns to the element
which assigns to the element 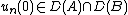 the value of the solution
the value of the solution  of the Cauchy problem (
of the Cauchy problem ( ) at the moment of time
) at the moment of time 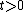 . If the Cauchy problem is well posed, then the operator
. If the Cauchy problem is well posed, then the operator  is defined on
is defined on 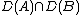 and forms a semigroup.
and forms a semigroup.
Additionally, if 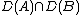 is dense in
is dense in  , the operator
, the operator  can be extended to a bounded linear operator defined on the entire space
can be extended to a bounded linear operator defined on the entire space  . In this case one can associate to any
. In this case one can associate to any 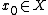 the function
the function 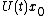 , for any
, for any 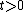 . Such a function is called generalized solution of the Cauchy problem.
. Such a function is called generalized solution of the Cauchy problem.
If 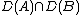 is dense in
is dense in  and the Cauchy problem is uniformly well posed, then the associated semigroup
and the Cauchy problem is uniformly well posed, then the associated semigroup  is a C0-semigroup in
is a C0-semigroup in  .
.
Conversely, if  is the infinitesimal generator of a C0-semigroup
is the infinitesimal generator of a C0-semigroup  , then the Cauchy problem
, then the Cauchy problem
is uniformly well posed and the solution is given by
Nonhomogeneous problem
The Cauchy problem
with  , is called nonhomogeneous when
, is called nonhomogeneous when 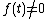 . The following theorem gives some sufficient conditions for the existence of the solution:
. The following theorem gives some sufficient conditions for the existence of the solution:
Theorem. If  is an infinitesimal generator of a C0-semigroup
is an infinitesimal generator of a C0-semigroup  and
and  is continuously differentiable, then the function
is continuously differentiable, then the function
is the unique solution to the (abstract) nonhomogeneous Cauchy problem.
The integral on the right-hand side as to be intended as a Bochner integral.
Time-dependent problem
The problem[7] of finding a solution to the initial value problem
where the unknown is a function 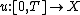 ,
, 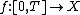 is given and, for each
is given and, for each 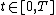 ,
, 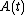 is a given, closed, linear operator in
is a given, closed, linear operator in  with domain
with domain  , independent of
, independent of  and dense in
and dense in  , is called time-dependent Cauchy problem.
, is called time-dependent Cauchy problem.
An operator valued function 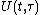 with values in
with values in 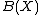 (the space of all bounded linear operators from
(the space of all bounded linear operators from  to
to  ), defined and strongly continuous jointly in
), defined and strongly continuous jointly in 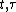 for
for 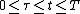 , is called a fundamental solution of the time-dependent problem if:
, is called a fundamental solution of the time-dependent problem if:
- the partial derivative
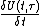 exists in the strong topology of
exists in the strong topology of  , belongs to
, belongs to 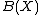 for
for 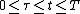 , and is strongly continuous in
, and is strongly continuous in  for
for 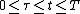 ;
; - the range of
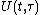 is in
is in  ;
;  and
and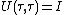 .
.
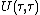 is also called evolution operator, propagator, solution operator or Green's function.
is also called evolution operator, propagator, solution operator or Green's function.
A function 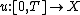 is called a mild solution of the time-dependent problem if it admits the integral representation
is called a mild solution of the time-dependent problem if it admits the integral representation
There are various known sufficient conditions for the existence of the evolution operator 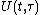 . In practically all cases considered in the literature
. In practically all cases considered in the literature 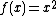 is assumed to be the infinitesimal generator of a C0-semigroup on
is assumed to be the infinitesimal generator of a C0-semigroup on  . Roughly speaking, if
. Roughly speaking, if 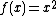 is the infinitesimal generator of a contraction semigroup the equation is said to be of hyperbolic type; if
is the infinitesimal generator of a contraction semigroup the equation is said to be of hyperbolic type; if 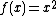 is the infinitesimal generator of an analytic semigroup the equation is said to be of parabolic type.
is the infinitesimal generator of an analytic semigroup the equation is said to be of parabolic type.
Non linear problem
The problem[7] of finding a solution to either
where 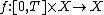 is given, or
is given, or
where  is a nonlinear operator with domain
is a nonlinear operator with domain 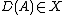 , is called nonlinear Cauchy problem.
, is called nonlinear Cauchy problem.
See also
- C0-semigroup
References
2. ^{{cite book |last1=Hille |first1=Einar |title=Functional Analysis And Semi Groups |date=1948 |publisher=American mathematical Society|url=https://archive.org/details/functionalanalys017173mbp}}
3. ^{{cite book |last1=Zaidman |first1=Samuel |title=Abstract differential equations |date=1979 |publisher=Pitman Advanced Publishing Program}}
4. ^{{cite book |last1=Krein |first1=Selim Grigorievich |title=Linear differential equations in Banach spaces |date=1972 |publisher=American Mathematical Society}}
5. ^{{cite book |last1=Zaidman |first1=Samuel |title=Topics in abstract differential equations |date=1994 |publisher=Longman Scientific & Technical}}
6. ^{{cite book |last1=Zaidman |first1=Samuel |title=Functional analysis and differential equations in abstract spaces |date=1999 |publisher=Chapman & Hall/CRC}}
7. ^1 {{cite book |last1=Lakshmikantham |first1=V. |last2=Ladas |first2=G. E. |title=Differential Equations in Abstract Spaces |date=1972}}
- Nellie Miller-Mann
- Nellie O'Malley
- Nellie Parker Spaulding
- Nellie Paulina Burgin
- Nellie Peters Black
- Nellie Rathbone Bright
- Nellie Robinson (politician)
- Nellie R. Santiago
- Nellie Saunders Allen
- Nellie Spicer
- Nellie Stone Johnson
- Nellie Takes Her Bow
- Nellie, the Beautiful Cloak Model
- Nellie Verrill Mighels Davis
- Nellie Wallace
- Nellie Winifred Bernice Schroder
- Nellie Yip Quong
- Nellie Zabel Willhite
- Nelli Feryabnikova
- Nelli Gorbatkova
- Nelliharvi
- Nellihudikeri
- Nellikani
- Nellikkode Bhaskaran
- Nellikkodu Bhaskaran