- Abstract economy with utility functions Definition Equilibrlium
- Exchange economy with utility functions Definition Equilibrium Reduction to abstract economy
- Abstract economy with preference correspondences Definition Equilibrium
- Exchange economy with preference correspondences Definition Equilibrium Reduction to abstract economy
- Welfare theorems in generalized abstract economies
- See also
- References
In theoretical economics, an abstract economy (also called a generalized N-person game) is a model that generalizes both the standard model of a exchange economy in microeconomics, and the standard model of a game in game theory. An equilibrium in an abstract economy generalizes both a competitive equilibrium in microeconomics, and a Nash equilibrium in game-theory.
The concept was introduced by Gérard Debreu in 1952. He named it generalized N-person game, and proved the existence of equilibrium in this game.[1] Later, Debreu and Kenneth Arrow (who renamed the concept to abstract economy) used this existence result to prove the existence of a competitive equilibrium in the Arrow–Debreu model.[2] Later, Shafer and Sonnenschein extended both theorems to irrational agents - agents with non-transitive and non-complete preferences.[3][4]
Abstract economy with utility functions
Definition
In the model of Debreu,[1] an abstract economy contains a finite number N of agents. For each agent 
, there is:
- A choice-set
(a subset of some Euclidean space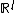 
). This represents the global set of choices that the agent can make.- We define the cartesian product of all choice sets as:
.
- We define the cartesian product of all choice sets as:
- An action-correspondence
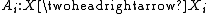. This represents the set of possible actions the agent can take, given the choices of the other agents. - A utility function:
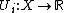, representing the utility that the agent receives from each combination of choices.
The goal of each agent is to choose an action that maximizes his utility.
Equilibrlium
An equilibrium in an abstract economy is a vector of choices, 
, such that, for each agent , the action 
maximizes the function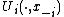 
subject to the constraint 
.
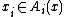The following conditions are sufficient for the existence of equilibrium:
- Each choice-set is compact, non-empty and convex.
- Each action-correspondence
is continuous, and its values are non-empty and convex. - Each utility function
is continuous on X and quasi-concave in .
Exchange economy with utility functions
Definition
An exchange economy is a system with N-1 consumers and 
homogeneous divisible goods. For each consumer i, there is:
- A consumption-set
(a subset of 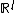). This represents the set of bundles that the agent can consume.- We define the cartesian product of all consumption sets as:
.
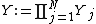- We define the cartesian product of all consumption sets as:
- An initial endowment vector
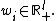
- A utility function
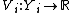. This represents the preferences of the agent.
Define the set of possible price-vectors as: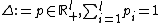 
.
Equilibrium
A competitive equilibrium in an exchange economy is a vector of consumption-bundles and a price-vector,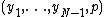 
, such that:
- The total consumption is at most the total endowment:
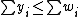. - The total expense of each agent is at most his budget:
. - For each agent , the consumption
maximizes the function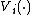 
subject to the constraint . I.e, if 
, then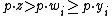 
.
Reduction to abstract economy
Arrow and Debreu[2] presented the following reduction from exchange economy to abstract economy.
Given an N-1-agent exchange economy, we define an N-agent abstract economy in which:
- Each of the first N-1 agents has choice set
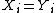, utility function 
, and action set defined by his budget: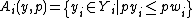 
. - The N-th agent, called a "market player", has a choice set
, utility function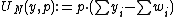 
, and action set defined by 
.
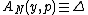The following conditions in the exchange economy are sufficient to guarantee that the abstract economy satisfies the conditions for equilibrium:
- Each consumption-set is compact and convex, and contains the endowment
in its interior. - Each utility function
is continuous and quasi-concave.
Moreover, the following additional condition is sufficient to guarantee that the equilibrium 
in the abstract economy corresponds to a competitive equilibrium in the exchange economy:
- For every agent i, is not a local (unconstrained) maximum of . For example, it is sufficient to assume that all agents are not satiated.
The definition 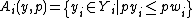guarantees that the total expense of each agent is at most his budget. The definition guarantees that the consumption of each agent maximizes his utility given the budget. And the definition 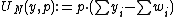guarantees that the total consumption is at most the total endowment.{{Why|date=January 2018}}
Therefore, if the exchange economy satisfies the above three conditions, a competitive equilibrium exists.
In the proof we assumed that depends only on , but this assumption is not really needed: the proof remains valid even if the utility depends on the consumptions of other agents (externalities), or on the prices.
Abstract economy with preference correspondences
Definition
In the generalized model of Shafer and Sonnenschein,[3] For each agent there is:
- A choice-set - as above;
- A constraint correspondence 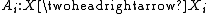- as above;
- Instead of a utility function there is a preference correspondence
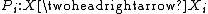. This represents, for each combination of choices of the other agents, what choices the agent strictly prefers to his current choice.
The model of Debreu is a special case of this model, in which the utility functions are defined as: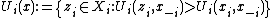 
. However, the generalized model does not require that the preference-correspondence can be represented by a utility function. In particular, it does not have to correspond to a transitive relation.
Equilibrium
An equilibrium in a generalized abstract economy is a vector of choices, , such that, for each agent , 
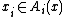and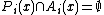 
. The equilibrium concept of Debreu is a special case of this equilibrium.
The following conditions are sufficient for the existence of equilibrium in the generalized abstract economy:[3]
- (a) Each choice-set is compact, non-empty and convex.
- (b') Each action-correspondence is continuous.
- (b'') The values
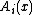are non-empty and convex for every x. - (c') Each preference-correspondence
has an open graph in 
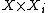(this is a form of continuity condition). - (c'') For each
, the convex hull of 
does not contain (this is a form of non-reflexivity condition: an agent does not strictly prefer a choice to itself).
Exchange economy with preference correspondences
Definition
Mas-Colell generalized the definition of exchange economy in the following way.[5] For every consumer i, there is:
- A consumption-set - as above;
- An initial endowment vector
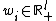- as above; - A preference relation
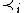that can be equivalently represented by a preference-correspondence: 
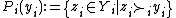. Note the preference relation is not required to be complete or transitive.
Equilibrium
A competitive equilibrium in such exchange economy is defined by:
- The sum of all prices is 1.
- The sum of all allocations is at most the sum of endowments .
- For every i:
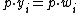. - For every bundle z: if
then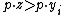 
(i.e, if the agent strictly prefers z to his share, then the agent cannot afford z).
Reduction to abstract economy
The same reduction shown above, from the exchange economy of Arrow-Debreu to the abstract economy of Debreu, can be done from the generalized exchange economy of Mas-Collel to the generalized abstract economy of Shafer-Sonnenschein. This reduction implies that the following conditions are sufficient for existence of competitive equilibrium in the generalized exchange economy:
- Each 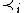is relatively-open (equivalently, each has an open graph);
- For every bundle x, the set is convex and does not contain x (= irreflexivity). Mas-Collel added the condition that the set is non-empty (= non-saturation).
- For every i:
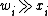for some bundle x (this means that the initial endowment is in the interior of the choice-sets).
Welfare theorems in generalized abstract economies
The welfare theorems can be extended to the above generalized abstract economies.[6]
See also
A further generalization of these equilibrium concepts can be found in Barabolla (1985).[7]
References
2. ^1 {{Cite journal|last=Arrow|first=Kenneth J.|last2=Debreu|first2=Gerard|date=1954|title=Existence of an Equilibrium for a Competitive Economy|jstor=1907353|journal=Econometrica|volume=22|issue=3|pages=265–290|doi=10.2307/1907353}}
3. ^1 2 {{Cite journal|date=1975-12-01|title=Equilibrium in abstract economies without ordered preferences|url=https://www.sciencedirect.com/science/article/pii/0304406875900026|journal=Journal of Mathematical Economics|volume=2|issue=3|pages=345–348|doi=10.1016/0304-4068(75)90002-6|issn=0304-4068}}
4. ^https://arxived.org/pdfs/files/425be847d31d3cc9665d00b8f0585038.pdf
5. ^{{Cite journal|last=Mas-Collel|first=Andrew|date=1974-12-01|title=An equilibrium existence theorem without complete or transitive preferences|url=https://www.sciencedirect.com/science/article/pii/0304406874900159|journal=Journal of Mathematical Economics|volume=1|issue=3|pages=237–246|doi=10.1016/0304-4068(74)90015-9|issn=0304-4068|via=}}
6. ^{{Cite journal|last=Vincy Fon and Yoshihiko Otani|first=|date=1979-06-01|title=Classical welfare theorems with non-transitive and non-complete preferences|url=https://www.sciencedirect.com/science/article/pii/0022053179900449|journal=Journal of Economic Theory|volume=20|issue=3|pages=409–418|doi=10.1016/0022-0531(79)90044-9|issn=0022-0531|via=}}
7. ^{{Cite journal|date=1985-01-01|title=Equilibrium and quasi-equilibrium existence theorems for a general model without ordered preferences|url=https://www.sciencedirect.com/science/article/pii/0165176585900229|journal=Economics Letters|volume=19|issue=3|pages=205–210|doi=10.1016/0165-1765(85)90022-9|issn=0165-1765}}
- Clarke, Rebecca
- Clarke-Riley diffusion flame
- Clark, Ernest
- Clarke, Robert
- Clarke, Rodney
- Clarke, Roger
- Clarke, Ronald
- Clarke, Rupert
- Clarke, Sarah
- Clarke Schmidt
- Clarke Scholtz
- Clarke's equation
- Clarkes Gardens
- Clarke's generalized Jacobian
- Clarkes Hill
- Clarkes Hill, Victoria
- Clarke, Simon
- Clarke's Laws
- Clarke's mining bee
- Clarkes of London
- Clarke & Spaulding
- Clarke, Spaulding & Howe
- Clarke, Steve
- Clarke, Steven
- Clarkesville, Ga.