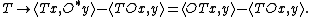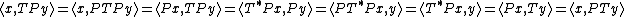“Von Neumann bicommutant theorem”的意思、由来-开放百科全书

词条

Von Neumann bicommutant theorem

释义

Proof
Proof of (i) Proof of (ii) Proof of (iii) Non-unital case
References

{{cleanup|reason=As mentioned on the talk page, the proof of item (iii) is incomplete.|date=September 2018}}

In mathematics, specifically functional analysis, the von Neumann bicommutant theorem relates the closure of a set of bounded operators on a Hilbert space in certain topologies to the bicommutant of that set. In essence, it is a connection between the algebraic and topological sides of operator theory.

The formal statement of the theorem is as follows:

Von Neumann Bicommutant Theorem. Let {{math|M}} be an algebra of bounded operators on a Hilbert space {{mvar|H}}, containing the identity operator and closed under taking adjoints. Then the closures of {{math|M}} in the weak operator topology and the strong operator topology are equal, and are in turn equal to the bicommutant {{math|M′′}} of {{math|M}}.{{clarify|Algebra of all bounded operators is undefined|date=February 2013}} This algebra is the von Neumann algebra generated by {{math|M}}.

There are several other topologies on the space of bounded operators, and one can ask what are the *-algebras closed in these topologies. If {{math|M}} is closed in the norm topology then it is a C*-algebra, but not necessarily a von Neumann algebra. One such example is the C*-algebra of compact operators (on an infinite dimensional Hilbert space). For most other common topologies the closed *-algebras containing 1 are still von Neumann algebras; this applies in particular to the weak operator, strong operator, *-strong operator, ultraweak, ultrastrong, and *-ultrastrong topologies.

It is related to the Jacobson density theorem.

Proof

Let {{mvar|H}} be a Hilbert space and {{math|L(H)}} the bounded operators on {{mvar|H}}. Consider a self-adjoint unital subalgebra {{math|M}} of {{math|L(H)}}. (this means that {{math|M}} contains the adjoints of its members, and the identity operator on {{mvar|H}})

The theorem is equivalent to the combination of the following three statements:

(i) {{math|cl_W(M) ⊆ M′′}}

(ii) {{math|cl_S(M) ⊆ cl_W(M)}}

(iii) {{math|M′′ ⊆ cl_S(M)}}

where the {{mvar|W}} and {{mvar|S}} subscripts stand for closures in the weak and strong operator topologies, respectively.

Proof of (i)

By definition of the weak operator topology, for any {{mvar|x}} and {{mvar|y}} in {{mvar|H}}, the map T → <Tx, y> is continuous in this topology. Therefore, for any operator {{mvar|O}} (and by substituting once {{math|y → O^∗y}} and once {{math|x → Ox}}), so is the map

Let S be any subset of {{math|L(H)}}, and S’ its commutant. For any operator {{mvar|T}} not in S’, <OTx, y> - <TOx, y> is nonzero for some O in S and some x and y in {{mvar|H}}. By the continuity of the abovementioned mapping, there is an open neighborhood of {{mvar|T}} in the weak operator topology for which this is nonzero, therefore this open neighborhood is also not in S’. Thus S’ is closed in the weak operator, i.e. S is weakly closed. Thus every commutant is weakly closed, and so is {{math|M′′}}; since it contains {{math|M}}, it also contains its weak closure.

Proof of (ii)

This follows directly from the weak operator topology being coarser than the strong operator topology: for every point {{mvar|x}} in {{math|cl_S(M)}}, every open neighborhood of {{mvar|x}} in the weak operator topology is also open in the strong operator topology and therefore contains a member of {{math|M}}; therefore {{mvar|x}} is also a member of {{math|cl_W(M)}}.

Proof of (iii)

Fix {{math|X ∈ M′′}}. We will show {{math|X ∈ cl_S(M)}}.

Fix an open neighborhood {{mvar|U}} of {{mvar|X}} in the strong operator topology. By definition of the strong operator topology, U contains a finite intersection U(h₁,ε₁) ∩...∩U(h_n,ε_n) of subbasic open sets of the form U(h,ε) = {O ∈ L(H): ||Oh - Xh|| < ε}, where h is in H and ε > 0.

Fix h in {{mvar|H}}. Consider the closure {{math|cl(Mh)}} of {{math|Mh {{=}} {Mh : M ∈ M}}} with respect to the norm of H and equipped with the inner product of H. It is a Hilbert space (being a closed subspace of a Hilbert space {{mvar|H}}), and so has a corresponding orthogonal projection which we denote {{mvar|P}}. {{mvar|P}} is bounded, so it is in {{math|L(H)}}. Next we prove:

Lemma. {{math|P ∈ M′}}.

Proof. Fix {{math|x ∈ H}}. Then {{math|Px ∈ cl(Mh)}}, so it is the limit of a sequence {{mvar|O_nh}} with {{mvar|O_n}} in {{math|M}} for all {{mvar|n}}. Then for all {{math|T ∈ M}}, {{mvar|TO_nh}} is also in {{math|Mh}} and thus its limit is in {{math|cl(Mh)}}. By continuity of {{mvar|T}} (since it is in {{math|L(H)}} and thus Lipschitz continuous), this limit is {{mvar|TPx}}. Since {{math|TPx ∈ cl(Mh)}}, PTPx = TPx. From this it follows that PTP = TP for all {{mvar|T}} in {{math|M}}.

By using the closure of {{math|M}} under the adjoint we further have, for every {{mvar|T}} in {{math|M}} and all {{math|x, y ∈ H}}:

thus TP = PT and P lies in {{math|M′}}.

By definition of the bicommutant XP = PX. Since {{math|M}} is unital, {{math|h ∈ Mh}}, hence {{math|Xh {{=}} XPh {{=}} PXh ∈ cl(Mh)}}. Thus for every {{math|ε > 0}}, there exists T in {{math|M}} with {{math|{{!!}}Xh − Th{{!!}} < ε}}. Then T lies in U(h,ε).{{clarify|reason=This part is incomplete since we must intersect a finite number of these subbasic open sets.|date=September 2015}}

Thus in every open neighborhood {{mvar|U}} of {{mvar|X}} in the strong operator topology there is a member of {{math|M}}, and so {{mvar|X}} is in the strong operator topology closure of {{math|M}}.

Non-unital case

An algebra {{math|M}}{{clarify|reason=What kind of algebra?|date=September 2015}} acting on H is said to act non-degenerately if for h in {{mvar|H}}, {{math|Mh {{=}} {0} }} implies {{math|h {{=}} 0}}. If {{math|M}} acts non-degenerately, and is a sub C*-algebra of {{math|L(H)}},{{clarify|reason=If M acts non-degenerately, it can be identified bijectively with its image A in L(H). Is the image being a sub-C*-algebra an additional hypothesis on the representation, or is it automatic at this point? The only obstacle I can see is being weakly closed, but maybe this is automatic.|date=September 2015}} it can be shown using an approximate identity in {{math|M}} that the identity operator I lies in the strong closure of {{math|M}}. Therefore, the conclusion of the bicommutant theorem still holds.

References

W.B. Arveson, An Invitation to C-algebras, Springer, New York, 1976.

4 : Operator theory|Von Neumann algebras|Articles containing proofs|Theorems in functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。