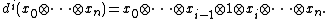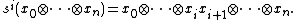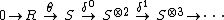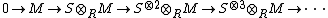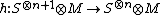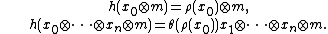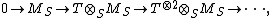“Amitsur complex”的意思、由来-开放百科全书

词条

Amitsur complex

释义

Definition
A theorem of Grothendieck
References
External links

In algebra, the Amitsur complex is a natural complex associated to a ring homomorphism that, when the homomorphism is a faithfully flat, is exact (thus determining a resolution). It was introduced in {{harv|Amitsur|1959}}.

The notion should be thought of as a mechanism to go beyond the conventional localization of rings and modules: see {{harv|M. Artin|loc=III.7.}}.

Definition

Let 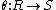be a homomorphism of (not-necessary-commutative) rings. First define the cosimplicial set 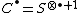as follows. Define the face maps 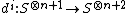by inserting 1 at the i-th spot:^[1]

Define the degeneracies 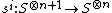by multiplying out the i-th and (i + 1)-th spots:

They satisfy the "obvious" cosimplicial identities and thus 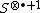is a cosimplicial set. It then determines the complex with the augumentation , the Amitsur complex:^[2]

where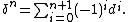

A theorem of Grothendieck

In the notations of #Definition, if is right faithfully flat, then a theorem of Grothendieck states that the (augmented) complex 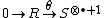is exact and thus is a resolution. More generally,^[3]

{{math_theorem|note=Grothendieck|math_statement=If

is right faithfully flat, then, for each left R-module M,

is exact.}}

Proof:

Step 1: The statement is true if 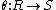splits as a ring homomorphism.

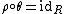That " splits" is to say for some homomorphism 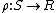( is a retraction and a section). Given such a , define

An easy computation shows the following identity: with ,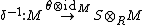

.

This is to say that h is a homotopy operator and so 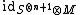determines the zero map on cohomology: i.e., the complex is exact.

Step 2: The statement is true in general.

We remark that 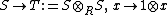is a section of 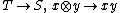. Thus, Step 1 applied to the split ring homomorphism 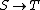implies:

where 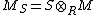, is exact. Since 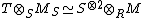, etc., by "faithfully flat", the original sequence is exact.

References

1. ^Note the reference (M. Artin) seems to have a typo, and this should be the correct formula; see the calculation of s⁰ and d² in the note.
2. ^{{harvnb|M. Artin|loc=III.6.}}
3. ^{{harvnb|M. Artin|loc=Theorem III.6.6.}}

M. Artin, noncommutative rings
Shimshon Amitsur, “Simple algebras and cohomology groups of arbitrary fields,” Transactions of the American Mathematical Society Vol. 90, No. 1 (Jan., 1959), pp. 73–112

External links

{{cite web|url=https://ncatlab.org/nlab/show/Amitsur+complex|website=ncatlab.org|title=Amitsur complex in nLab|accessdate=2018-12-22}}

1 : Algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。