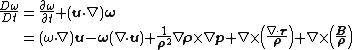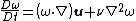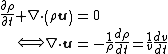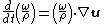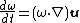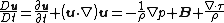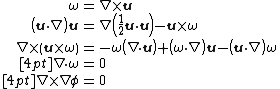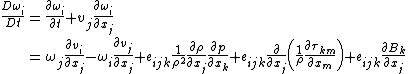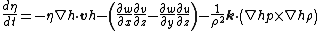“Vorticity equation”的意思、由来-开放百科全书

词条

Vorticity equation

释义

Physical interpretation
Simplifications
Derivation
Tensor notation
In specific sciences
Atmospheric sciences
See also
References

The vorticity equation of fluid dynamics describes evolution of the vorticity {{math|ω}} of a particle of a fluid as it moves with its flow, that is, the local rotation of the fluid (in terms of vector calculus this is the curl of the flow velocity).

The equation is:

where {{math|{{sfrac|D|Dt}}}} is the material derivative operator, {{math|u}} is the flow velocity, {{mvar|ρ}} is the local fluid density, {{mvar|p}} is the local pressure, {{mvar|τ}} is the viscous stress tensor and {{math|B}} represents the sum of the external body forces. The first source term on the right hand side represents vortex stretching.

The equation is valid in the absence of any concentrated torques and line forces, for a compressible Newtonian fluid.

In the case of incompressible (i.e. low Mach number) and isotropic fluids, with conservative body forces, the equation simplifies to the vorticity transport equation

where {{mvar|ν}} is the kinematic viscosity and {{math|∇²}} is the Laplace operator.

Physical interpretation

The term {{math|{{sfrac|Dω|Dt}}}} on the left-hand side is the material derivative of the vorticity vector {{math|ω}}. It describes the rate of change of vorticity of the moving fluid particle. This change can be attributed to unsteadiness in the flow ({{math|{{sfrac|∂ω|∂t}}}}, the unsteady term) or due to the motion of the fluid particle as it moves from one point to another ({{math|(u ∙ ∇)ω}}, the convection term).
The term {{math|(ω ∙ ∇) u}} on the right-hand side describes the stretching or tilting of vorticity due to the flow velocity gradients. Note that {{math|(ω ∙ ∇) u}} is a vector quantity, as {{math|ω ∙ ∇}} is a scalar differential operator, while {{math|∇u}} is a nine-element tensor quantity.
The term {{math|ω(∇ ∙ u)}} describes stretching of vorticity due to flow compressibility. It follows from the Navier-Stokes equation for continuity, namely

where {{math|v {{=}} {{sfrac|1|ρ}}}} is the specific volume of the fluid element. One can think of {{math|∇ ∙ u}} as a measure of flow compressibility. Sometimes the negative sign is included in the term.

The term {{math|{{sfrac|1|ρ²}}∇ρ × ∇p}} is the baroclinic term. It accounts for the changes in the vorticity due to the intersection of density and pressure surfaces.
The term {{math|∇ × ({{sfrac|∇ ∙ τ|ρ}})}}, accounts for the diffusion of vorticity due to the viscous effects.
The term {{math|∇ × B}} provides for changes due to external body forces. These are forces that are spread over a three-dimensional region of the fluid, such as gravity or electromagnetic forces. (As opposed to forces that act only over a surface (like drag on a wall) or a line (like surface tension around a meniscus).

Simplifications

In case of conservative body forces, {{math|∇ × B {{=}} 0}}.
For a barotropic fluid, {{math|∇ρ × ∇p {{=}} 0}}. This is also true for a constant density fluid (including incompressible fluid) where {{math|∇ρ {{=}} 0}}. Note that this is not the same as an incompressible flow, for which the barotropic term cannot be neglected.
For inviscid fluids, the viscosity tensor {{mvar|τ}} is zero.

Thus for an inviscid, barotropic fluid with conservative body forces, the vorticity equation simplifies to

Alternately, in case of incompressible, inviscid fluid with conservative body forces,

For a brief review of additional cases and simplifications, see also.^[1]

Derivation

The vorticity equation can be derived from the Navier–Stokes equation for the conservation of angular momentum. In the absence of any concentrated torques and line forces, one obtains

Now, vorticity is defined as the curl of the flow velocity vector. Taking the curl of momentum equation yields the desired equation.

The following identities are useful in derivation of the equation:

where {{mvar|ϕ}} is any scalar field.

Tensor notation

The vorticity equation can be expressed in tensor notation using Einstein's summation convention and the Levi-Civita symbol {{mvar|e_ijk}}:

In specific sciences

Atmospheric sciences

In the atmospheric sciences, the vorticity equation can be stated in terms of the absolute vorticity of air with respect to an inertial frame, or of the vorticity with respect to the rotation of the Earth. The absolute version is

Here, {{mvar|η}} is the polar ({{mvar|z}}) component of the vorticity, {{mvar|ρ}} is the atmospheric density, {{mvar|u}}, {{mvar|v}}, and w are the components of wind velocity, and {{math|∇_h}} is the 2-dimensional (i.e. horizontal-component-only) del.

References

1. ^{{cite web|first=K. P.|last=Burr |title=Marine Hydrodynamics, Lecture 9|website=MIT Lectures|url=http://web.mit.edu/2.20/www/lectures/2016/Lecture_9_2016.pdf}}

{{cite journal | first1= Utpal |last1=Manna |first2=S. S. |last2=Sritharan | title= Lyapunov Functionals and Local Dissipativity for the Vorticity Equation in {{mvar|L{{isup|p}}}} and Besov spaces | journal = Differential and Integral Equations | volume= 20 |number =5 |year= 2007|pages= 581–598}}
{{cite book|first1=V. |last1=Barbu |first2=S. S. |last2=Sritharan |chapter={{mvar|M}}-Accretive Quantization of the Vorticity Equation |title=Semi-Groups of Operators: Theory and Applications |editor-first=A. V. |editor-last=Balakrishnan |publisher=Birkhauser |location=Boston |date=2000 |pages=296–303 |chapter-url=http://www.nps.edu/Academics/Schools/GSEAS/SRI/BookCH12.pdf}}
{{cite journal|first=A. M. |last=Krigel |title=Vortex evolution |journal=Geophysical, Astrophysical Fluid Dynamics |date=1983 |volume=24 |pages=213–223}}

1 : Equations of fluid dynamics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。