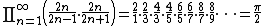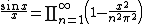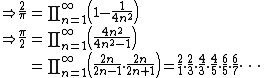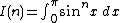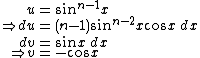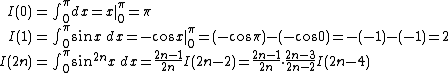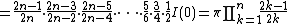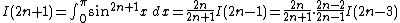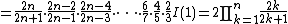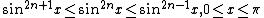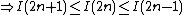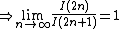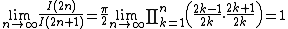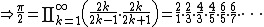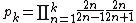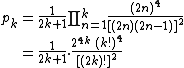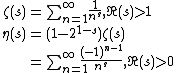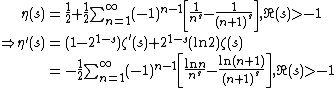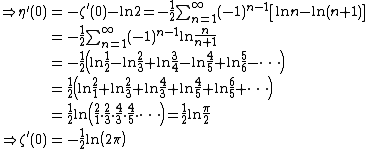“Wallis product”的意思、由来-开放百科全书

词条

Wallis product

释义

Derivation
Proof using Euler's infinite product for the sine function^[1]
Proof using integration^[2]
Relation to Stirling's approximation
ζ'(0)^[1]
See also
Notes
External links

In mathematics, Wallis' product for {{pi}}, written down in 1655 by John Wallis, states that

{{comparison_pi_infinite_series.svg|400px|the Wallis product (purple asterisks) and}}

Derivation

Wallis derived this infinite product as it is done in calculus books today, by examining 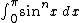for even and odd values of n, and noting that for large n, increasing n by 1 results in a change that becomes ever smaller as n increases. Since modern infinitesimal calculus did not yet exist then, and the mathematical analysis of the time was inadequate to discuss the convergence issues, this was a hard piece of research, and tentative as well.

Wallis' product is, in retrospect, an easy corollary of the later Euler formula for the sine function.

Proof using Euler's infinite product for the sine function^[1]

Let x = {{sfrac|{{pi}}|2}}:

Proof using integration^[2]

Let:

(a form of Wallis' integrals).

Integrate by parts:

This result will be used below:

Repeating the process,

, from above results.

By the squeeze theorem,

Relation to Stirling's approximation

Stirling's approximation for n! asserts that

.

Consider now the finite approximations to the Wallis product, obtained by taking the first k terms in the product:

p_k can be written as

Substituting Stirling's approximation in this expression (both for k! and (2k)!) one can deduce (after a short calculation) that p_k converges to {{frac|π|2}} as k → ∞.

ζ'(0)^[1]

The Riemann zeta function and the Dirichlet eta function can be defined:

Applying an Euler transform to the latter series, the following is obtained:

Notes

1. ^¹{{cite web|url=http://mathworld.wolfram.com/WallisFormula.html|title=Wallis Formula}}
2. ^{{cite web|url=http://www.sosmath.com/calculus/integration/powerproduct/problem/problem.html|title=Integrating Powers and Product of Sines and Cosines: Challenging Problems}}

External links

{{springer|title=Wallis formula|id=p/w097040}}
{{cite web |date=April 20, 2018 |title=Why does this product equal π/2? A new proof of the Wallis formula for π. |url=https://www.youtube.com/watch?v=8GPy_UMV-08 |via=YouTube|publisher=3Blue1Brown}}

2 : Articles containing proofs|Pi algorithms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Derivation

Proof using Euler's infinite product for the sine function[1]

Proof using integration[2]