“Arithmetic progression game”的意思、由来-开放百科全书

词条

Arithmetic progression game

释义

References

The arithmetic progression game is a positional game where two players alternately pick numbers, trying to occupy a complete arithmetic progression of a given size.

The game is parameterized by two integers n > k. The game-board is the set {1,...,n}. The winning-sets are all the arithmetic progressions of length k. In the common Maker-Breaker variant, the first player (Maker) wins by occupying a k-length arithmetic progression, otherwise the second player (Breaker) wins.

The game is also called the van der waerden game,^[1] named after Van der Waerden's theorem. It says that, for any k, there exists some integer W(2,k) such that, if the integers {1, ..., W(2,k)} are partitioned arbitrarily into two sets, then at least one set contains an arithmetic progression of length k. This means that, if 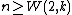, then Maker has a winning strategy.

Unfortunately, this claim is not constructive - it does not show a specific strategy for Maker. Moreover, the current upper bound for W(2,k) is extremely large (the currently known bounds are: ).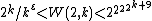

Let W*(2,k) be the smallest integer such that Maker has a winning strategy. Beck ^[1] proves that 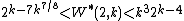. In particular, if 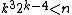, then the game is Maker's win (even though it is much smaller than the number that guarantees no-draw).

References

1. ^¹{{Cite journal|last=Beck|first=József|date=1981|title=Van der waerden and ramsey type games|journal=Combinatorica|language=en|volume=1|issue=2|pages=103–116|doi=10.1007/bf02579267|issn=0209-9683}}

1 : Positional games

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。