“Automorphism group”的意思、由来-开放百科全书

词条

Automorphism group

释义

Examples
In category theory
Automorphism group functor
See also
References
External links

{{short description|Mathematical group formed from the automorphisms of an object}}

In mathematics, the automorphism group of an object X is the group consisting of automorphisms of X. For example, if X is a finite-dimensional vector space, then the automorphism group of X is the general linear group of X, the group of invertible linear transformations from X to itself.

Especially in geometric contexts, an automorphism group is also called a symmetry group. A subgroup of an automorphism group is called a transformation group (especially in old literature).

Examples

The automorphism group of a set X is precisely the symmetric group of X.
A group homomorphism to the automorphism group of a set X amounts to a group action on X: indeed, each left G-action on a set X determines , and, conversely, each homomorphism 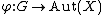defines an action by .
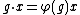Let be two finite sets of the same cardinality and 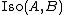the set of all bijections 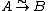. Then 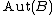, which is a symmetric group (see above), acts on 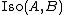from the left freely and transitively; that is to say, 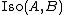is a torsor for 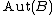(cf. #In category theory).
The automorphism group of a finite cyclic group of order n is isomorphic to 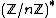with the isomorphism given by .^[1] In particular, is an abelian group.
Given a field extension 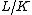, the automorphism group of it is the group consisting of field automorphisms of L that fixes K: it is better known as the Galois group of .
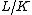The automorphism group of the projective n-space over a field k is the projective linear group 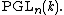^[2]
The automorphism group of a finite-dimensional real Lie algebra has the structure of a (real) Lie group (in fact, it is even a linear algebraic group: see below). If G is a Lie group with Lie algebra , then the automorphism group of G has a structure of a Lie group induced from that on the automorphism group of .^[3]^[4]
Let P be a finitely generated projective module over a ring R. Then there is an embedding 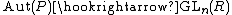, unique up to inner automorphisms.^[5]

In category theory

Automorphism groups appear very natural in category theory.

If X is an object in a category, then the automorphism group of X is the group consisting of all the invertible morphisms from X to itself. It is the unit group of the endomorphism monoid of X. (For some example, see PROP.)

If are objects in some category, then the set 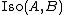of all 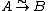is a left 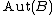-torsor. In practical terms, this says that a different choice of a base point of 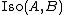differs unambiguously by an element of 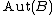, or that each choice of a base point is precisely a choice of a trivialization of the torsor.

If 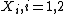are objects in categories 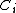and if 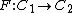is a functor that maps 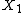to 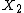, then the functor induces a group homomorphism 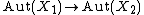, as it maps invertible morphisms to invertible morphisms.

In particular, if G is a group viewed as a category with a single object * or, more generally, if G is a groupoid, then each functor 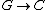, C a category, is called an action or a representation of G on the object 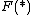, or the objects 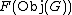. Those objects are then said to be -objects (as they are acted by ); cf. -object. If is a module category like the category of finite-dimensional vector spaces, then -objects are also called -modules.

Automorphism group functor

Let be a finite-dimensional vector space over a field k that is equipped with some algebraic structure (that is, M is a finite-dimensional algebra over k). It can be, for example, an associative algebra or a Lie algebra.

Now, consider k-linear maps 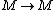that preserve the algebraic structure: they form a vector subspace 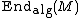of 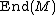. The unit group of 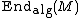is the automorphism group 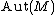. When a basis on M is chosen, 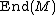is the space of square matrices and 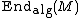is the zero set of some polynomial equations and the invertibility is again described by polynomials. Hence, 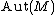is a linear algebraic group over k.

Now base extensions applied to the above discussion determines a functor:^[6] namely, for each commutative ring R over k, consider the R-linear maps 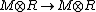preserving the algebraic structure: denote it by 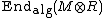. Then the unit group of the matrix ring 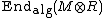over R is the automorphism group 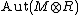and 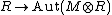is a group functor: a functor from the category of commutative rings over k to the category of groups. Even better, it is represented by a scheme (since the automorphism groups are defined by polynomials): this scheme is called the automorphism group scheme and is denoted by .

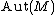In general, however, an automorphism group functor may not be represented by a scheme.

References

1. ^{{harvnb|Dummit|Foote|loc=§ 2.3. Exercise 26.}}
2. ^{{harvnb|Hartshorne|loc=Ch. II, Example 7.1.1.}}
3. ^{{Cite journal |jstor = 1990752|title = The Automorphism Group of a Lie Group|journal = Transactions of the American Mathematical Society|volume = 72|issue = 2|pages = 209–216|last1 = Hochschild|first1 = G.|year = 1952}}
4. ^(following {{harvnb|Fulton–Harris|loc=Exercise 8.28.}}) First, if G is simply connected, the automorphism group of G is that of

. Second, every connected Lie group is of the form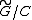

where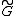

is a simply connected Lie group and C is a central subgroup and the automorphism group of G is the automorphism group of

that preserves C. Third, by convention, a Lie group is second countable and has at most coutably many connected components; thus, the general case reduces to the connected case.
5. ^{{harvnb|Milnor|loc=Lemma 3.2.}}
6. ^{{harvnb|Waterhouse|loc=§ 7.6.}}

{{cite book | last1=Dummit | first1=David S. | last2=Foote | first2=Richard M. | title=Abstract Algebra | publisher=John Wiley & Sons | year=2004 | edition=3rd | isbn=978-0-471-43334-7}}
{{Fulton-Harris}}
{{Hartshorne AG}}
{{Citation | last1=Milnor | first1=John Willard | author1-link= John Milnor | title=Introduction to algebraic K-theory | publisher=Princeton University Press | location=Princeton, NJ | mr=0349811 | year=1971 | zbl=0237.18005 | series=Annals of Mathematics Studies | volume=72}}
William C. Waterhouse, Introduction to Affine Group Schemes, Graduate Texts in Mathematics vol. 66, Springer Verlag New York, 1979.

External links

https://mathoverflow.net/questions/55042/automorphism-group-of-a-scheme

1 : Group automorphisms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Examples

In category theory

Automorphism group functor

See also

References

External links