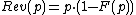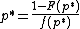- Single item and single buyer
- Single item and many buyers Buyers with independent and identical valuations Buyers with independent and different valuations
- Different items and one unit-demand buyer
- Different items and many unit-demand buyers Many unit-demand buyers and sellers
- See also
- References
Bayesian-optimal pricing (BO pricing) is a kind of algorithmic pricing in which a seller determines the sell-prices based on probabilistic assumptions on the valuations of the buyers. It is a simple kind of a Bayesian-optimal mechanism, in which the price is determined in advance without collecting actual buyers' bids.
Single item and single buyer
In the simplest setting, the seller has a single item to sell (with zero cost), and there is a single potential buyer. The highest price that the buyer is willing to pay for the item is called the valuation of the buyer. The seller would like to set the price exactly at the buyer's valuation. Unfortunately, the seller does not know the buyer's valuation. In the Bayesian model, it is assumed that the buyer's valuation is a random variable drawn from a known probability distribution.
Suppose the cumulative distribution function of the buyer is 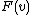 , defined as the probability that the seller's valuation is less than
, defined as the probability that the seller's valuation is less than  . Then, if the price is set to
. Then, if the price is set to  , the expected value of the seller's revenue is:[1]
, the expected value of the seller's revenue is:[1]
because the probability that the buyer will want to buy the item is 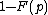 , and if this happens, the seller's revenue will be
, and if this happens, the seller's revenue will be  .
.
The seller would like to find the price that maximizes 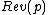 . The first-order condition, that the optimal price
. The first-order condition, that the optimal price 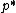 should satisfy, is:
should satisfy, is:
where 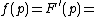 the probability density function.
the probability density function.
For example, if the probability distribution of the buyer's valuation is uniform in 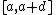 , then
, then 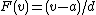 and
and 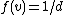 (in
(in 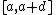 ). The first-order condition is
). The first-order condition is 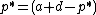 which implies
which implies 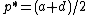 . This is the optimal price only if it is in the range
. This is the optimal price only if it is in the range 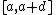 (i.e., when
(i.e., when 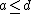 ).
).
Otherwise (when 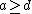 ), the optimal price is
), the optimal price is 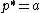 .
.
This optimal price has an alternative interpretation: it is the solution to the equation:
where  is the virtual valuation of the agent. So in this case, BO pricing is equivalent to the Bayesian-optimal mechanism, which is an auction with reserve-price
is the virtual valuation of the agent. So in this case, BO pricing is equivalent to the Bayesian-optimal mechanism, which is an auction with reserve-price 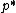 .
.
Single item and many buyers
In this setting, the seller has a single item to sell (with zero cost), and there are multiple potential buyers whose valuations are a random vector drawn from some known probability distribution. Here, different pricing methods come to mind:[2]
- Symmetric prices: the seller sets a single price for the item. If one or more buyers accept this price, then one of them is selected arbitrarily.
- discriminatory prices: the seller sets a different price for each buyer. If one or more buyers accept this price, then the buyer who accepted the highest price is selected. Discriminatory pricing can be implemented sequentially by ordering the prices in decreasing order and giving the item to the first buyer who accepts the price offered to him.
In the multiple-buyer setting, BO pricing is no longer equivalent to BO auction: in pricing, the seller has to determine the price/s in advance, while in auction, the seller can determine the price based on the agents' bids. The competition between the buyers may enable the auctioneer to raise the price. Hence, in theory, the seller can obtain a higher revenue in an auction.
Example.[3] There are two buyers whose valuations are distributed uniformly in the range 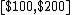 .
.
- The BO auction is the Vickrey auction with reserve price $100 (= the inverse-virtual-valuation of 0). Its expected revenue is $133.
- The BO discriminatory pricing scheme is to offer one agent a price of $150 and the other agent a price of $100. Its expected revenue is 0.5150 + 0.5100 = $125.
In practice, however, an auction is more complicated for the buyers since it requires them to declare their valuation in advance. The complexity of the auction process might deter buyers and ultimately lead to loss of revenue.[2][3] Therefore, it is interesting to compare the optimal pricing revenue to the optimal auction revenue, to see how much revenue the seller loses by using the simpler mechanism.
Buyers with independent and identical valuations
Blumrosen and Holenstein[4] study the special case in which the buyers' valuations are random variables drawn independently from the same probability distribution. They show that, when the distribution of the buyers' valuations has bounded support, BO-pricing and BO-auction converge to the same revenue. The convergence rate is asymptotically the same when discriminatory prices are allowed, and slower by a logarithmic factor when symmetric prices must be used. For example, when the distribution is uniform in [0,1] and there are  potential buyers:
potential buyers:
- the revenue of the BO auction (a Vickrey auction with reserve price determined by the probability distribution) is
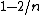 ;
; - the revenue of BO discriminatory pricing is
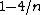 ;
; - the revenue of BO symmetric pricing is
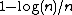 .
.
In contrast, when the distribution of the buyers' valuations has unbounded support, the BO-pricing and the BO-auction might not converge to the same revenue. E.g., when the cdf is 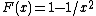 :
:
- the revenue of the BO auction is
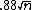 ;
; - the revenue of BO discriminatory pricing is
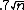 ;
; - the revenue of BO symmetric pricing is
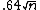 .
.
Buyers with independent and different valuations
Chawla and Hartline and Malec and Sivan[5] study the setting in which the buyers' valuations are random variables drawn independently from different probability distributions. Moreover, there are constraints on the set of agents that can be served together (for example: there is a limited number of units). They consider two kinds of discriminatory pricing schemes:
- In an order-oblivious pricing mechanism (OPM), the mechanism-designer determines a price for each agent. The agents come in an arbitrary order. The mechanism guarantees are for worst-case (adversarial) order of the agents, determined after the agents' valuations are drawn.
- In a sequential pricing mechanism (SPM), the mechanism-designer determines both a price for each agent, and an ordering on the agents. The mechanism loops over the agents in the pre-determined order. If the current agent can be served together with the previously-served agents (according to the constraints), then his personal price is offered to him, and he can either take it or leave it.
Their general scheme for calculating the prices is:
- For each agent
 , calculate the probability
, calculate the probability 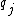 with which the BO mechanism (Myerson's mechanism) serves agent
with which the BO mechanism (Myerson's mechanism) serves agent  . This can be calculated either analytically or by simulations.
. This can be calculated either analytically or by simulations. - The price for agent
 is
is 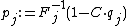 , where
, where  is a constant (either 1 or 1/2 or 1/3, depending on the setting). In other words, the price
is a constant (either 1 or 1/2 or 1/3, depending on the setting). In other words, the price  satisfies the following condition:
satisfies the following condition:
Prob[the valuation of agentis at least
] =
Prob[the BO mechanism serves agent
].
If 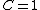 then the marginal-probability that an agent is served by the SPM is equal to the marginal-probability that it is served by the BO auction.
then the marginal-probability that an agent is served by the SPM is equal to the marginal-probability that it is served by the BO auction.
The approximation factors obtainable by an OPM depend on the structure of the constraints:[5]{{rp|318}}
- uniform matroid or partition matroid constraints - 2 (i.e, the revenue of the BO OPM is at least 1/2 the revenue of Myerson's BO auction).
- graphic matroid - 3
- Intersection of two partition matroids - 6.75
- Intersection of a graphic matroid and a partition matroid - 10.66
- General matroid with matroid rank
 -
- 
Moreover, they show two lower bounds:
- An OPM cannot guarantee more than 1/2 the revenue of the BO auction, even in the single-item setting.
- An OPM cannot guarantee more than
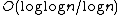 the revenue of the BO auction when there are downwards-closed non-matroid constraint.
the revenue of the BO auction when there are downwards-closed non-matroid constraint.
The approximation factors obtainable by an SPM are naturally better:
- Uniform matroid, partition matroid - e/(e-1) ≅ 1.58
- General matroid - 2
- Intersection of two matroids - 3
The lower bound (proved by [4]) is approximately 1.25.
Yan[6] explains the success of the sequential-pricing approach based on the concept of correlation gap, in the following way. The revenue of a mechanism is related to a set function  . E.g, in a k-unit auction, the function is
. E.g, in a k-unit auction, the function is 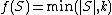
- The revenue of the BO auction is at most
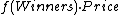 , where "Winners" is the set of k agents with highest valuations.
, where "Winners" is the set of k agents with highest valuations. - The revenue of the BO SPM is at least
 , where "Demand" is the set of agents whose valuation is above the price.
, where "Demand" is the set of agents whose valuation is above the price.
Both "Winners" and "Demand" are random-sets, determined by the agents' valuations. Moreover, by carefully setting the price, it is possible to ensure that each agent  has the same probability
has the same probability 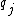 to be in "Winners" and to be in "Demand". However, in "Winners", there is high correlation between different agents (if one agent wins, there is more probability that other agents lose), while in "Demand", the agents are independent. Therefore, the correlation gap is an upper bound on the loss of performance when using BO SPM instead of BO auction. This gives the following approximation factors:
to be in "Winners" and to be in "Demand". However, in "Winners", there is high correlation between different agents (if one agent wins, there is more probability that other agents lose), while in "Demand", the agents are independent. Therefore, the correlation gap is an upper bound on the loss of performance when using BO SPM instead of BO auction. This gives the following approximation factors:
- General matroid -
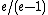
- k-unit auctions (a sub-case of general matroids) -
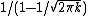
- p-independent set systems (a generalization of the intersection of
 matroids) -
matroids) -  .
.
Different items and one unit-demand buyer
In this setting, the seller has several different items for sale (e.g. cars of different models). There is one potential buyer, that is interested in a single item (e.g. a single car). The buyer has a different valuation for each item-type (i.e., he has a valuation-vector). Given the posted prices, the buyer buys the item that gives him the highest net utility (valuation minus price).
The buyer's valuation-vector is a random-vector from a multi-dimensional probability distribution. The seller wants to compute the price-vector (a price per item) that gives him the highest expected revenue.
Chawla and Hartline and Kleinberg[7] study the case in which the buyer's valuations to the different items are independent random variables. They show that:
- The revenue of the BO unit-demand pricing when there are
 item-types is at most the revenue of the BO single-item auction when there are
item-types is at most the revenue of the BO single-item auction when there are  potential buyers.
potential buyers. - When the buyer's valuations to the different items are independent draws from the same distribution, the BO unit-demand pricing that uses the same price to all items attains at least 1/2.17 of the revenue of the BO single-item auction.[8]
- When the buyer's valuations are independent draws from different distributions, the BO unit-demand pricing that uses the same virtual-price (based on virtual valuations) attains at least 1/3 of the revenue of the BO single-item auction.
They also consider the computational task of calculating the optimal price. The main challenge is to calculate 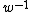 , the inverse of the virtual valuation function.
, the inverse of the virtual valuation function.
- For discrete and regular valuation distribution, there is a polynomial-time 3-approixmation.
- For continuous and regular valuation distribution (available via an oracle) there is a polynomial-time (3+ε)-approximation with high probability, and a faster (6+ε)-approximation with probability 1.
Different items and many unit-demand buyers
In this setting, there are different types of items. Each buyer has different valuations for different items, and each buyer wants at most one item. Moreover, there are pre-specified constraints on the set of buyer-item pairs that can be allocated together (for example: each item can be allocated to at most one buyer; each buyer can get at most one item; etc).
Chawla and Hartline and Malec and Sivan[5] study two kinds of discriminatory pricing schemes:
- In a sequential pricing mechanism (SPM), the mechanism-designer determines a price for each buyer-item pair, and an ordering on the buyer-item pairs. The mechanism loops over the buyer-item pairs in the pre-determined order. If the current buyer-item pair is feasible, then the buyer is offered the item in the pre-determined price, and he can either take it or leave it.
- In an order-oblivious pricing mechanism (OPM), the mechanism-designer determines a price for each buyer-item pair. The buyers come in an arbitrary order, which may be adversarially determined after the agents' valuations are drawn.
A sequential-pricing mechanism is, in general, not a truthful mechanism, since an agent may decide to decline a good offer in hopes of getting a better offer later. It is truthful only when, for every buyer, the buyer-item pairs for that buyer are ordered in decreasing order of net-utility. Then, it is always best for the buyer to accept the first offer (if its net utility is positive). A special case of that situation is the single-parameter setting: for every buyer, there is only a single buyer-item pair (e.g, there is a single item for sale).
To every multi-parameter setting corresponds a single-parameter setting in which each buyer-item pair is considered an independent agent. In the single-parameter setting, there is more competition (since the agents that come from the same buyer compete with each other). Therefore, the BO revenue in the single-parameter setting is an upper bound on the BO revenue in the multi-parameter setting. Therefore, if an OPM is an r-approximation to the optimal mechanism for a single-parameter setting, then it is also an r-approximation to the corresponding multi-parameter setting.[5] See above for approximation factors of OPMs in various settings.
See Chapter 7 "Multi-dimensional Approximation" in [9]{{rp|124}} for more details.
Many unit-demand buyers and sellers
Recently, the SPM scheme has been extended to a double auction setting, where there are both buyers and sellers. The extended mechanism is called 2SPM. It is parametrized by an order on the buyers, an order on the sellers, and a matrix of prices - a price for each buyer-seller pair. The prices are offered to in order to buyers and sellers who may either accept or reject the offer. The approximation ratio is between 3 and 16, depending on the setting.[10]
See also
- Monopoly pricing
References
2. ^{{cite book|doi=10.7551/mitpress/9780262033428.003.0002|chapter=The Lovely but Lonely Vickrey Auction|title=Combinatorial Auctions|pages=17|year=2005|last1=Ausubel|first1=Lawrence M.|last2=Milgrom|first2=Paul|isbn=9780262033428}}
3. ^{{cite web | url=https://www.bloomberg.com/news/articles/2008-06-03/auctions-on-ebay-a-dying-breedbusinessweek-business-news-stock-market-and-financial-advice | title=Auctions on eBay: A Dying Breed | date=June 3, 2008 | accessdate=1 July 2016 | author=Catherine Holahan}}
4. ^1 2 {{cite conference|doi=10.1145/1386790.1386801|chapter=Posted prices vs. Negotiations|title=Proceedings of the 9th ACM conference on Electronic commerce - EC '08|pages=49|year=2008|last1=Blumrosen|first1=Liad|last2=Holenstein|first2=Thomas|isbn=9781605581699|url=http://citeseerx.ist.psu.edu/viewdoc/download?rep=rep1&type=pdf&doi=10.1.1.221.9912}}
5. ^1 2 3 4 {{cite conference|doi=10.1145/1806689.1806733|chapter=Multi-parameter mechanism design and sequential posted pricing|title=Proceedings of the 42nd ACM symposium on Theory of computing - STOC '10|pages=311|year=2010|last1=Chawla|first1=Shuchi|author1-link= Shuchi Chawla |last2=Hartline|first2=Jason D.|last3=Malec|first3=David L.|last4=Sivan|first4=Balasubramanian|isbn=9781450300506|arxiv=0907.2435}}
6. ^{{cite conference|doi=10.1137/1.9781611973082.56|chapter=Mechanism Design via Correlation Gap|title=Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms|pages=710|year=2011|last1=Yan|first1=Qiqi|isbn=978-0-89871-993-2|arxiv=1008.1843}}
7. ^{{cite conference|doi=10.1145/1250910.1250946|chapter=Algorithmic pricing via virtual valuations|title=Proceedings of the 8th ACM conference on Electronic commerce - EC '07|pages=243|year=2007|last1=Chawla|first1=Shuchi|author1-link= Shuchi Chawla |last2=Hartline|first2=Jason D.|last3=Kleinberg|first3=Robert|isbn=9781595936530|arxiv=0808.1671}}
8. ^Single-price pricing is not necessarily the optimal pricing. For example, suppose there are two items, each with a value independently equal to 1 with probability 2/3 and 2 with probability 1/3. Then, the price-vectors (1,2) and (2,1) are optimal, but the price-vectors (1,1) and (2,2) are sub-optimal.
9. ^{{cite book | url=https://jeremy-chen.org/sites/default/files/files/convexset/2012_11/amd.pdf | title=Approximation in Economic Design| author=Jason D. Hartline | year=2012}}
10. ^{{cite conference|doi=10.1137/1.9781611974331.ch98 |chapter=Approximately Efficient Double Auctions with Strong Budget Balance |title=Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms |pages=1424 |year=2016 |last1=Colini-Baldeschi |first1=Riccardo |last2=Keijzer |first2=Bart de |last3=Leonardi |first3=Stefano |last4=Turchetta |first4=Stefano |isbn=978-1-61197-433-1 }}
- National Tsaotun Commercial & Industrial Senior High School
- National Tsing Hua University Nan Da Campus
- National Tsunami Warning Center
- National Tuberculosis Institute
- National Tulip Day
- National Tyre Distributors Association
- National Tyre Distributors Association (NTDA)
- National tyres
- National Tyres and Autocare
- National Under 20 Rugby Championship
- National Underclassmen Combine
- National Underground Railroad Network to Freedom
- National Unification Advisory Council
- National Unification Day
- National Unification Guidelines
- National Union Attack
- National Union Building
- National Union Fire Insurance Company of Pittsburgh, PA
- National Union for Democracy and Rally
- National Union for Democracy in the Comoros
- National Union for Democratic Progress
- National Union for Social Justice (organization)
- National Union for Solidarity and Development
- National Union for Solidarity and Progress
- National Union from Banat