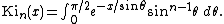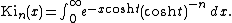“Bickley–Naylor functions”的意思、由来-开放百科全书

词条

Bickley–Naylor functions

释义

Definition
Properties
See also
References

In physics, engineering, and applied mathematics, the Bickley–Naylor functions are a sequence of special functions arising in formulas for thermal radiation intensities in hot enclosures. The solutions are often quite complicated unless the problem is essentially one-dimensional^[1] (such as the radiation field in a thin layer of gas between two parallel rectangular plates). These functions have practical applications in several engineering problems related to transport of thermal^[2]^[3] or neutron^[4] radiation in systems with special symmetries (e.g. spherical or axial symmetry). W. G. Bickley was a British mathematician born in 1893.^[5]

Definition

The nth Bickley−Naylor function Ki_n(x) is defined by

and it is classified as one of the generalized exponential integral functions.

Properties

The integral defining the function Ki_n generally cannot be evaluated analytically, but can be approximated to a desired accuracy with Riemann sums or other methods, taking the limit as a → 0 in the interval of integration, [a, {{pi}}/2].

Alternative ways to define the function Ki_n include the integral^[6]

All of the functions Ki_n for positive integer n are monotonously decreasing functions, because e^−x is a decreasing function and 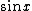is a positive increasing function for .

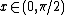The values of these functions for different values of the argument x were often listed in tables of special functions in the era when numerical calculation of integrals was slow. A table that lists some approximate values of the three first functions Ki_n is shown below.

x	Ki₁(x)	Ki₂(x)	Ki₃(x)
0	1.57	1.00	0.79
0.2	1.02	0.75	0.61
0.4	0.75	0.58	0.48
0.6	0.56	0.45	0.38
0.8	0.43	0.35	0.30
1.0	0.33	0.27	0.24
1.2	0.25	0.22	0.19
1.4	0.20	0.17	0.15
1.6	0.16	0.14	0.12
1.8	0.12	0.11	0.10

References

1. ^Michael F. Modest, Radiative Heat Transfer, p. 282, Elsevier Science 2003
2. ^Zekerya Altaḉ, Exact series expansions, recurrence relations, properties and integrals of the generalized exponential integral functions, Journal of Quantitative Spectroscopy & Radiative Transfer 104 (2007) 310–325
3. ^Z. Altaç, Integrals Involving Bickley and Bessel Functions in Radiative Transfer, and Generalized Exponential Integral Functions, J. Heat Transfer 118(3), 789−792 (August 1, 1996)
4. ^T. Boševski, An Improved Collision Probability Method for Thermal-Neutron-Flux Calculation in a Cylindrical Reactor Cell, NUCLEAR SCIENCE AND ENGINEERING:. 42, 23−27 (1970)
5. ^G. S. Marliss W. A. Murray, William G. Bickley—An appreciation, Comput J (1969) 12 (4): 301–302.
6. ^A. Baricz, T. K. Pogany, Functional Inequalities for the Bickley Function, Mathematical Inequalities and Applications, Volume 17, Number 3 (2014), 989–1003

1 : Special functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Properties

See also

References