“Bing–Borsuk conjecture”的意思、由来-开放百科全书

In mathematics, the Bing–Borsuk conjecture states that every

-dimensional homogeneous absolute neighborhood retract space is a topological manifold. The conjecture has been proved for dimensions 1 and 2, and it is known that the 3-dimensional version of the conjecture implies the Poincaré conjecture.

Definitions

A topological space is homogeneous if, for any two points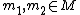

, there is a homeomorphism of

which takes

A metric space

is an absolute neighborhood retract (ANR) if, for every closed embedding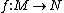

(where

is a metric space), there exists an open neighbourhood

of the image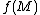

which retracts to

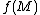.^[1]

There is an alternate statement of the Bing–Borsuk conjecture: suppose

is embedded in

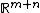for some

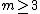and this embedding can be extended to an embedding of

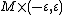. If

has a mapping cylinder neighbourhood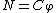

of some map

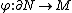with mapping cylinder projection

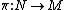, then

is an approximate fibration.^[2]

History

The conjecture was first made in a paper by R. H. Bing and Karol Borsuk in 1965, who proved it for

and 2.^[3]

Włodzimierz Jakobsche showed in 1978 that, if the Bing–Borsuk conjecture is true in dimension 3, then the Poincaré conjecture must also be true.^[4]

The Busemann conjecture states that every Busemann

-space is a topological manifold. It is a special case of the Bing–Borsuk conjecture. The Busemann conjecture is known to be true for dimensions 1 to 4.

References

1. ^{{cite journal|last1=M.|first1=Halverson, Denise|last2=Dušan|first2=Repovš,|title=The Bing–Borsuk and the Busemann conjectures|journal=Mathematical Communications|date=23 December 2008|volume=13|issue=2|url=https://hrcak.srce.hr/30884|language=en|issn=1331-0623}}
2. ^{{cite journal|last1=Daverman|first1=R. J.|last2=Husch|first2=L. S.|title=Decompositions and approximate fibrations.|journal=The Michigan Mathematical Journal|date=1984|volume=31|issue=2|pages=197–214|doi=10.1307/mmj/1029003024|url=https://projecteuclid.org/euclid.mmj/1029003024|language=en|issn=0026-2285}}
3. ^{{cite book|last1=Bing|first1=R. H.|last2=Armentrout|first2=Steve|title=The Collected Papers of R. H. Bing|date=1998|publisher=American Mathematical Soc.|isbn=9780821810477|pages=167|url=https://books.google.com/books?id=NnBQ0xp_rUcC&pg=PA167|language=en}}
4. ^{{cite journal|last1=Jakobsche|first1=W.|title=The Bing–Borsuk conjecture is stronger than the Poincaré conjecture|journal=Fundamenta Mathematicae|volume=106|issue=2|url=https://eudml.org/doc/211089|language=en|issn=0016-2736}}