“Binomial process”的意思、由来-开放百科全书

词条

Binomial process

释义

Definition
Properties
Name Laplace-transform Intensity measure
Generalizations
Literature

A binomial process is a special point process in probability theory.

Definition

Let be a probability distribution and be a fixed natural number. Let be i.i.d. random variables with distribution , so for all .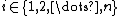

Then the binomial process based on n and P is the random measure

Properties

Name

The name of a binomial process is derived from the fact that for all measurable sets the random variable follows a binomial distribution with parameters and :

Laplace-transform

The Laplace transform of a binomial process is given by

for all positive measurable functions .

Intensity measure

The intensity measure of a binomial process is given by

Generalizations

A generalization of binomial processes are mixed binomial processes. In these point processes, the number of points is not deterministic like it is with binomial processes, but is determined by a random variable . Therefore mixed binomial processes conditioned on are binomial process based on and .

Literature

{{cite book |last1=Kallenberg |first1=Olav |author-link1=Olav Kallenberg |year=2017 |title=Random Measures, Theory and Applications|location= Switzerland |publisher=Springer |doi= 10.1007/978-3-319-41598-7|isbn=978-3-319-41596-3}}

1 : Point processes

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。