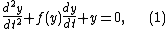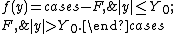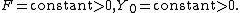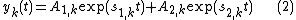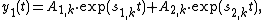- References
}}The Biryukov equation (or Biryukov oscillator), named after Vadim Biryukov (1946), is a non-linear second-order differential equation used to model damped oscillators.[1]
The equation is given by
where ƒ(y) is a piecewise constant function which is positive, except for small y as
Eq. (1) is a special case of the Lienard equation; it describes the auto-oscillations.
Solution (1) at a separate time intervals when f(y) is constant is given by[2]
Here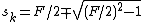 
, at 
and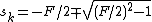 
otherwise. Expression (2) can be used for real and complex values of 
.
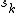The first half-period’s solution at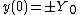 
is
The second half-period’s solution is
The solution contains four constants of integration 
, 
, 
, 
, the period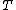 
and the boundary 
between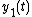 
and 
needs to be found. A boundary condition is derived from continuity of 
) and 
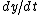.[3]
Solution of (1) in the stationary mode thus is obtained by solving a system of algebraic equations as
; 
; 
; 
;
;
.
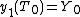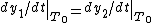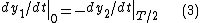The integration constants are obtained by the Levenberg–Marquardt algorithm.
With 
, 
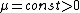, Eq. (1) named Van der Pol oscillator. Its solution cannot be expressed by elementary functions in closed form.
References
2. ^Arrowsmith D. K., Place C. M. Dynamical Systems. Differential equations, maps and chaotic behavior. Chapman & Hall, (1992)
3. ^Pilipenko A. M., and Biryukov V. N. «Investigation of Modern Numerical Analysis Methods of Self-Oscillatory Circuits Efficiency», Journal of Radio Electronics, No 9, (2013). http://jre.cplire.ru/jre/aug13/9/text-engl.html
- Carterus
- Carter v Burr
- Carter v. Canada
- Carter v. Canada (AG)
- Carter v Canada (AG)
- Carter v. Carter Coal Company
- Carter v Carter Coal Company
- Carter V. Findley
- Carterville Formation
- Carterville Marching Lions
- Carterville, Montana
- Carter-Wallace
- Carter Walton
- Carter, William
- Carter, Wisconsin
- Carter, Wisconsin (disambiguation)
- Carter Wong
- Carter Work Project
- Carter–Gilmer House
- Carter–Jones House
- Carter–Swain House
- Carter–Terry–Call House
- Carter–Worth House and Farm
- Cartes de visite
- Cartes (disambiguation)