- Block Bases Theorem 1. Proof Block Fourier Basis Discrete Block Bases Theorem 2. Block Bases of Images
- References
}}
Wavelet packet bases are designed by dividing the frequency axis in intervals of varying sizes. These bases are particularly well adapted to decomposing signals that have different behavior in different frequency intervals. If 
has properties that vary in time, it is then more appropriate to decompose in a block basis that segments the time axis in intervals with sizes that are adapted to the signal structures.
Block Bases
Block orthonormal bases are obtained by dividing the time axis in consecutive intervals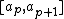 
with
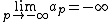and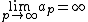 
.
The size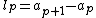 
of each interval is arbitrary. Let 
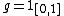. An interval is covered by the dilated rectangular window
Theorem 1. constructs a block orthogonal basis of 
from a single orthonormal basis of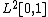 
.
Theorem 1.
if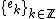 
is an orthonormal basis of 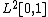, then
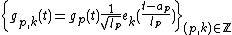
is a block orthonormal basis of
Proof
One can verify that the dilated and translated family
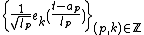
is an orthonormal basis of 
. If 
, then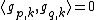 
since their supports do not overlap. Thus, the family 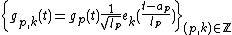is orthonormal. To expand a signal in this family, it is decomposed as a sum of separate blocks
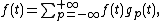
and each block 
is decomposed in the basis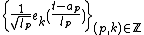
Block Fourier Basis
A block basis is constructed with the Fourier basis of :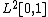
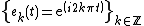
The time support of each block Fourier vector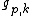 
is 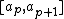of size 
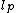. The Fourier transform of 
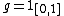is
and
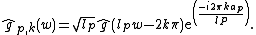
It is centered at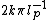 
and has a slow asymptotic decay proportional to 
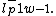Because of this poor frequency localization, even though a signal is smooth, its decomposition in a block Fourier basis may include large high-frequency coefficients. This can also be interpreted as an effect of periodization.
Discrete Block Bases
For all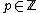 
, we suppose that 
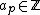. Discrete block bases are built with discrete rectangular windows having supports on intervals 
:
.
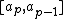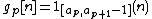Since dilations are not defined in a discrete framework,we generally cannot derive bases of intervals of varying sizes from a single basis. Thus,Theorem 2. supposes that we can construct an orthonormal basis of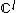 
for any 
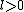. The proof is straightforward.
Theorem 2.
Suppose that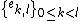 
is an orthogonal basis of 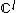for any 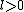. The family
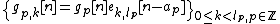
is a block orthonormal basis of 
.
A discrete block basis is constructed with discrete Fourier bases
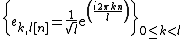
The resulting block Fourier vectors 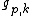have sharp transitions at the window border, and thus are not well localized in frequency. As in the continuous case, the decomposition of smooth signals may produce large-amplitude, high-frequency coefficients because of border effects.
Block Bases of Images
General block bases of images are constructed by partitioning the plane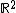 
into rectangles 
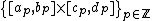of arbitrary length 
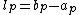and width 
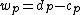. Let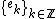 
be an orthonormal basis of 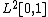and 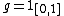. We denote
.
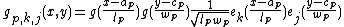The family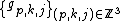 
is an orthonormal basis of 
.
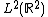For discrete images,we define discrete windows that cover each rectangle
.
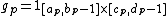If 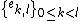is an orthogonal basis of 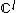for any 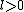, then
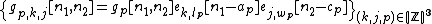
is a block basis of 
References
- St´ephane Mallat, A Wavelet Tour of Signal Processing, 3rd
- Northern Lights (song)
- Northern Light (sternwheeler)
- Northern Light (whiskey)
- Northern Lightz
- Northern Limit Line (film)
- Northern linanthus
- Northern Lincolnshire and Goole Hospitals NHS Foundation Trust
- Northern Line Embankment, High Barnet
- Northern line extension
- Northern Line extension
- Northern Line Extension
- Northern Line Extension to Nine Elms and Battersea
- Northern Line (IZBAN)
- Northern line (Sri Lanka)
- Northern Line (Thailand)
- Northern little penguin
- Northern Little Yellow-eared Bat
- Northern Ljubljana Bypass
- Northern Logrunner
- Northern Loloish
- Northern Loloish languages
- Northern Long-eared Bat
- Northern long-eared bats
- Northern long-eared owl
- Northern Lorung language