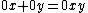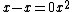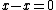“Wheel theory”的意思、由来-开放百科全书

词条

Wheel theory

释义

Definition
Algebra of wheels
Wheel of fractions
Citations
References

Wheels are a type of algebra where division is always defined. In particular, division by zero is meaningful. The real numbers can be extended to a wheel, as can any commutative ring.

The Riemann sphere can also be extended to a wheel by adjoining an element , where 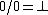. The Riemann sphere is an extension of the complex plane by an element , where for any complex . However, 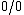is still undefined on the Riemann sphere, but is defined in its extension to a wheel.

The term wheel is inspired by the topological picture 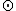of the projective line together with an extra point .{{sfn|Carlström|2004}}

Definition

A wheel is an algebraic structure , satisfying:

Addition and multiplication are commutative and associative, with and as their respective identities.

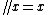
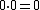
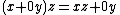
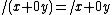
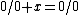
Algebra of wheels

Wheels replace the usual division as a binary operator with multiplication, with a unary operator applied to one argument 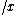similar (but not identical) to the multiplicative inverse , such that becomes shorthand for , and modifies the rules of algebra such that

in the general case
in the general case
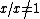in the general case, as 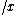is not the same as the multiplicative inverse of .

If there is an element such that 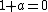, then we may define negation by and .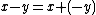

Other identities that may be derived are

And, for with and 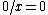, we get the usual

If negation can be defined as above then the subset is a commutative ring, and every commutative ring is such a subset of a wheel. If is an invertible element of the commutative ring, then . Thus, whenever makes sense, it is equal to 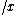, but the latter is always defined, even when .

Wheel of fractions

Let be a commutative ring, and let be a multiplicative submonoid of . Define the congruence relation on via

means that there exist such that .

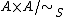Define the wheel of fractions of with respect to as the quotient (and denoting the equivalence class containing as ) with the operations

{{in5|10}}(additive identity)

{{in5|10}}(multiplicative identity)

{{in5|10}}(reciprocal operation)

{{in5|10}}(addition operation)

{{in5|10}}(multiplication operation)

Citations

References

{{citation |year=1997 |last=Setzer|first=Anton |title=Wheels |url=http://www.cs.swan.ac.uk/~csetzer/articles/wheel.pdf }} (a draft)
{{citation |year=2004 |last=Carlström|first=Jesper |title=Wheels – On Division by Zero |journal=Mathematical Structures in Computer Science |doi=10.1017/S0960129503004110 |volume=14 |issue=1 |publisher=Cambridge University Press |pages=143–184 }} (also available online here).

1 : Abstract algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。