1. Definition

2. Strategies

3. References

A box-making game (often called just a box game) is a biased positional game where two players alternately pick elements from a family of pairwise-disjoint sets ("boxes"). The first player - called BoxMaker - tries to pick all elements of a single box. The second player - called BoxBreaker - tries to pick at least one element of all boxes.

The box game was first presented by Paul Erdős and Václav Chvátal.^[1] It was solved later by Hamidoune and Las-Vergnas.^[2]

Definition

A box game is defined by:

• A family of n pairwise-disjoint sets, , of different sizes. The sets are often called "boxes" and the elements are called "balls".
• Two integers, p and q.

The first player, BoxMaker, picks p balls (from the same or different boxes). Then the second player, BoxBreaker, breaks q boxes. And so on.

BoxMaker wins if he has managed to pick all balls in at least one box, before BoxBreaker managed to break this box. BoxBreaker wins if he has managed to break all the boxes.

Strategies

In general, the optimal strategy for BoxBreaker is to break the boxes with the smallest number of remaining elements. The optimal strategy for BoxMaker is to try to balance the sizes of all boxes. By simulating these strategies, Hamidoune and Las-Vergnas^[2] found a sufficient and necessary condition for each player in the (p:q) box game.

For the special case where q=1, the each of the following conditions is sufficient:^[3]{{Rp|36-39}}

• If all boxes have the same size k, and 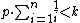, then BoxBreaker wins the (p:1) box game (using the obvious strategy of breaking the smallest boxes). For comparison, the winning condition for Breaker in a general (p:q) biased game is: 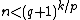. With q=1 this becomes . The proof uses a potential function. The potential of the game before BoxBreaker's j-th move is defined as: where is the number of elements remaining in box i.
• If the boxes have different sizes k1,...,kn, and 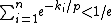, then BoxBreaker wins the (p:1) box game. For comparison, the winning condition for Breaker in a general (p:q) biased game is: 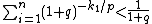. With q=1 this becomes .

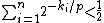References

• Schwar
• Schwarczenberger
• Schwa (restaurant)
• Schwarm
• Schwarmstedt, Germany
• Schwartenberg
• Schwartz and gross
• Schwartz Avi
• Schwartzbard's trial
• Schwartz-Bruhat function
• Schwartz-Burgess Syndrome
• Schwartz class
• Schwartz Cove
• Schwartze Mansion
• Schwartzenberg
• Schwartzenberger
• Schwartzentruber Amish
• Schwartz functions
• Schwartz Gyorgy
• Schwartz György
• Schwartzhog
• Schwartziella
• Schwartziella abacocubensis
• Schwartziella abundata
• Schwartziella angularis