“Whitney immersion theorem”的意思、由来-开放百科全书

词条

Whitney immersion theorem

释义

Further results
See also
References
External links

In differential topology, the Whitney immersion theorem states that for , any smooth -dimensional manifold (required also to be Hausdorff and second-countable) has a one-to-one immersion in Euclidean -space, and a (not necessarily one-to-one) immersion in 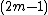-space. Similarly, every smooth -dimensional manifold can be immersed in the -dimensional sphere (this removes the constraint).

The weak version, for 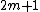, is due to transversality (general position, dimension counting): two m-dimensional manifolds in 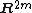intersect generically in a 0-dimensional space.

Further results

Massey went on to prove that every n-dimensional manifold is cobordant to a manifold that immerses in 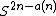where 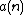is the number of 1's that appear in the binary expansion of . In the same paper, Massey proved that for every n there is manifold (which happens to be a product of real projective spaces) that does not immerse in 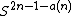. The conjecture that every n-manifold immerses in 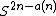became known as the Immersion Conjecture which was eventually solved in the affirmative by Ralph Cohen {{Harv|Cohen|1985}}.

References

{{citation

|doi=10.2307/1971304
|first=Ralph L.
|last=Cohen
|title=The Immersion Conjecture for Differentiable Manifolds
|journal=The Annals of Mathematics
|year=1985
|pages=237–328
|jstor=1971304
|volume=122
|issue=2
|publisher=Annals of Mathematics
}}

External links

Stiefel-Whitney Characteristic Classes and the Immersion Conjecture, by Jeffrey Giansiracusa, 2003

Exposition of Cohen's work

1 : Theorems in differential topology

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Further results

See also

References

External links