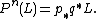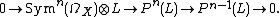- See also
- References
In algebraic geometry, given a line bundle L on a smooth variety X, the bundle of n-th order principal parts of L is a vector bundle of rank n + 1 that, roughly, parametrizes n-th order Taylor expansions of sections of L.
Precisely, let I be the ideal sheaf defining the diagonal embedding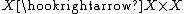 
and 
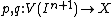the restrictions of projections 
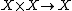to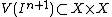 
. Then the bundle of n-th order principal parts is[1]
Then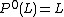 
and there is a natural exact sequence of vector bundles[2]
where 
is the sheaf of differential one-forms on X.
See also
- Linear system of divisors (bundles of principal parts can be used to study the oscillating behaviors of a linear system.)
- Jet (mathematics) (a closely related notion)
References
1. ^{{harvnb|Fulton|loc=Example 2.5.6.}}
2. ^{{harvnb|SGA 6|loc=Exp II, Appendix II 1.2.4.}}
2. ^{{harvnb|SGA 6|loc=Exp II, Appendix II 1.2.4.}}
- {{Citation | title=Intersection theory | publisher=Springer-Verlag | location=Berlin, New York | series=Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. | isbn=978-3-540-62046-4 | mr=1644323 | year=1998 | volume=2 | edition=2nd | author=William Fulton.}}
- Appendix II of Exp II of {{cite book
| editor-last = Berthelot
| editor-first = Pierre
| editor-link = Pierre Berthelot (mathematician)
| editor2=Alexandre Grothendieck
| editor3=Luc Illusie
| title = Séminaire de Géométrie Algébrique du Bois Marie - 1966-67 - Théorie des intersections et théorème de Riemann-Roch - (SGA 6) (Lecture notes in mathematics 225)
| year = 1971
| publisher = Springer-Verlag
| location = Berlin; New York
| language = French
| pages = xii+700
| nopp = true
|doi=10.1007/BFb0066283
|isbn= 978-3-540-05647-8
| mr = 0354655
}}{{algebraic-geometry-stub}}
1 : Algebraic geometry
- Cotton effect
- Cottonera Lines
- Cotton Exchange
- Cotton-Eyed
- Cotton Eyed Joe
- Cotton eye joe
- Cotton-Eye Joe
- Cotton Eye Joe
- Cotton Factor
- Cotton factor
- Cotton famine
- Cotton Fields
- Cotton Fields (The Cotton Song)
- Cotton-gin
- Cotton ginning
- Cottongrass
- Cotton-grass
- Cotton grass
- Cotton Ground
- Cotton Harvester
- Cotton harvester
- Cotton Hill Township, Sangamon County, Illinois
- Cottonian
- Cottonian Annals
- Cottonian Collection