- See also
- References
In mathematics in general, a characterization theorem says that a particular object – a function, a space, etc. – is the only one that possesses properties specified in the theorem. A characterization of a probability distribution accordingly states that it is the only probability distribution that satisfies specified conditions. More precisely, the model of characterization of
probability distribution was described by [https://ru.wikipedia.org/wiki/%D0%97%D0%BE%D0%BB%D0%BE%D1%82%D0%B0%D1%80%D1%91%D0%B2,_%D0%92%D0%BB%D0%B0%D0%B4%D0%B8%D0%BC%D0%B8%D1%80_%D0%9C%D0%B8%D1%85%D0%B0%D0%B9%D0%BB%D0%BE%D0%B2%D0%B8%D1%87 V.M. Zolotarev] [1] in such manner. On the probability space we define the space 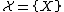 of random variables with values in measurable metric space
of random variables with values in measurable metric space 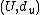 and the space
and the space 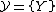 of random variables with values in measurable metric space
of random variables with values in measurable metric space 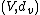 . By characterizations of probability distributions we understand general problems of description of some set
. By characterizations of probability distributions we understand general problems of description of some set  in the space
in the space 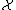 by extracting the sets
by extracting the sets 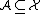 and
and 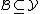 which describe the properties of random variables
which describe the properties of random variables  and their images
and their images 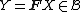 , obtained by means of a specially chosen mapping
, obtained by means of a specially chosen mapping 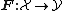 .
.
The description of the properties of the random variables 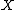 and of their images
and of their images 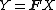 is equivalent to the indication of the set
is equivalent to the indication of the set 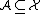 from which
from which 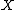 must be taken and of the set
must be taken and of the set 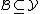 into which its image must fall. So, the set which interests us appears therefore in the following form:
into which its image must fall. So, the set which interests us appears therefore in the following form:
where 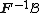 denotes the complete inverse image of
denotes the complete inverse image of  in
in 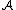 . This is the general model of characterization of probability distribution. Some examples of characterization theorems:
. This is the general model of characterization of probability distribution. Some examples of characterization theorems:
- The assumption that two linear (or non-linear) statistics are identically distributed (or independent, or have a constancy regression and so on) can be used to characterize various populations.[2] For example, according to George Pólya's [3] characterization theorem, if
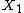 and
and 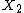 are independent identically distributed random variables with finite variance, then the statistics
are independent identically distributed random variables with finite variance, then the statistics 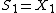 and
and 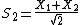 are identically distributed if and only if
are identically distributed if and only if 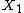 and
and 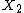 have a normal distribution with zero mean. In this case
have a normal distribution with zero mean. In this case
,
is a set of random two-dimensional column-vectors with independent identically distributed components,
is a set of random two-dimensional column-vectors with identically distributed components and
is a set of two-dimensional column-vectors with independent identically distributed normal components.
- According to generalized George Pólya's characterization theorem (without condition on finiteness of variance [2]) if
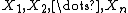 are non-degenerate independent identically distributed random variables, statistics
are non-degenerate independent identically distributed random variables, statistics 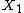 and
and 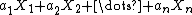 are identically distributed and
are identically distributed and 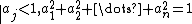 , then
, then  is normal random variable for any
is normal random variable for any 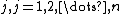 . In this case
. In this case
,
is a set of random n-dimensional column-vectors with independent identically distributed components,
is a set of random two-dimensional column-vectors with identically distributed components and
is a set of n-dimensional column-vectors with independent identically distributed normal components.[4]
- All probability distributions on the half-line
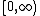 that are memoryless are exponential distributions. "Memoryless" means that if
that are memoryless are exponential distributions. "Memoryless" means that if 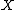 is a random variable with such a distribution, then for any numbers
is a random variable with such a distribution, then for any numbers 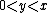 ,
,
.
Verification of conditions of characterization theorems in practice is possible only with some error  , i.e., only to a certain degree of accuracy.[5] Such a situation is observed, for instance, in the cases where a sample of finite size is considered. That is why there arises the following natural question. Suppose that the conditions of the characterization theorem are fulfilled not exactly but only approximately. May we assert that the conclusion of the theorem is also fulfilled approximately? The theorems in which the problems of this kind are considered are called stability characterizations of probability distributions.
, i.e., only to a certain degree of accuracy.[5] Such a situation is observed, for instance, in the cases where a sample of finite size is considered. That is why there arises the following natural question. Suppose that the conditions of the characterization theorem are fulfilled not exactly but only approximately. May we assert that the conclusion of the theorem is also fulfilled approximately? The theorems in which the problems of this kind are considered are called stability characterizations of probability distributions.
See also
- Characterization (mathematics)
References
2. ^1 A. M. Kagan, Yu. V. Linnik and C. Radhakrishna Rao (1973). [https://www.researchgate.net/publication/44720749_Characterization_problems_in_mathematical_statistics_by_A_M_Kagan_Yu_V_Linnik_and_C_Radhakrishna_Raotranslated_from_Russian_text_by_B_Ramachandran Characterization Problems in Mathematical Statistics]. John Wiley and Sons, New York, XII+499 pages.
3. ^Pólya, Georg (1923)."Herleitung des Gaußschen Fehlergesetzes ans einer Funktionalgleichung". Mathematische Zeitschrift. 18: 96–108. {{ISSN|0025-5874}}; 1432–1823.
4. ^R. Yanushkevichius.[https://www.academia.edu/24648381/R.Yanushkevichius._Stability_characterizations_of_distributions._1 Stability for characterizations of distributions.] Vilnius, Mokslas, 1991.
5. ^R. Yanushkevichius.[https://www.academia.edu/24648382/R.Yanushkevichius._Stability_characterizations_of_distributions._2 Stability characterizations of some probability distributions.] Saarbrücken, LAP LAMBERT Academic Publishing, 2014.
- Katenluy-e Sofla
- Kate Nolan
- Kate Noll
- Kate Novak-Grubb
- Kate Næss
- Kate Ní Cnaimhín
- Kate O'Brian
- Kate O'Brien
- Kate O'Brien (cyclist)
- Kate O'Brien (disambiguation)
- Kate O'Brien (The Drew Carey Show)
- Kate O'Connor
- Kate O'Hanlon
- Kate Okikiolu
- Kate O'Neill
- Kate Orff
- Kate Osamor
- Kate Otten
- Kate O’Brien
- Katepally
- Katepally, Nalgonda district
- Kate Palmer (disambiguation)
- Kate Palmer (netball)
- Kate Pang
- Katepanikia