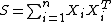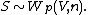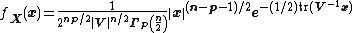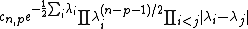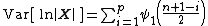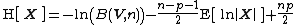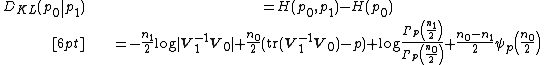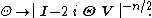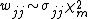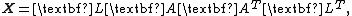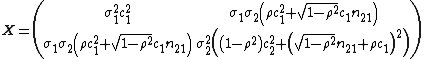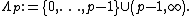- Definition
- Occurrence
- Probability density function
- Use in Bayesian statistics Choice of parameters
- Properties Log-expectation Log-variance Entropy Cross-entropy KL-divergence Characteristic function
- Theorem Corollary 1 Corollary 2
- Estimator of the multivariate normal distribution
- Bartlett decomposition
- Marginal distribution of matrix elements
- The range of the shape parameter
- Relationships to other distributions
- See also
- References
- External links
| name =Wishart
| type =density
| pdf_image =
| cdf_image =
| notation ={{math|X ~ Wp(V, n)}}
| parameters ={{math|n > p − 1}} degrees of freedom (real)
{{math|V > 0}} scale matrix ({{math|p × p}} pos. def)
| support ={{math|X(p × p)}} positive definite matrix
| pdf =
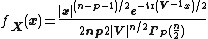
- {{math|Γp}} is the multivariate gamma function
- {{math|tr}} is the trace function
| cdf =
| mean =
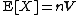 |
|| median =
| mode ={{math|(n − p − 1)V}} for {{math|n ≥ p + 1}}
| variance =

| skewness =
| kurtosis =
| entropy =see below
| mgf =
| char =

}}
In statistics, the Wishart distribution is a generalization to multiple dimensions of the gamma distribution. It is named in honor of John Wishart, who first formulated the distribution in 1928.[1]
It is a family of probability distributions defined over symmetric, nonnegative-definite matrix-valued random variables (“random matrices”). These distributions are of great importance in the estimation of covariance matrices in multivariate statistics. In Bayesian statistics, the Wishart distribution is the conjugate prior of the inverse covariance-matrix of a multivariate-normal random-vector.
Definition
Suppose {{mvar|X}} is an {{math|p × n}} matrix, each column of which is independently drawn from a {{mvar|p}}-variate normal distribution with zero mean:
Then the Wishart distribution is the probability distribution of the {{math|p × p}} random matrix
known as the scatter matrix. One indicates that {{mvar|S}} has that probability distribution by writing
The positive integer {{mvar|n}} is the number of degrees of freedom. Sometimes this is written {{math|W(V, p, n)}}. For {{math|n ≥ p}} the matrix {{mvar|S}} is invertible with probability {{math|1}} if {{mvar|V}} is invertible.
If {{math|p {{=}} V {{=}} 1}} then this distribution is a chi-squared distribution with {{mvar|n}} degrees of freedom.
Occurrence
The Wishart distribution arises as the distribution of the sample covariance matrix for a sample from a multivariate normal distribution. It occurs frequently in likelihood-ratio tests in multivariate statistical analysis. It also arises in the spectral theory of random matrices{{Citation needed|date=October 2010}} and in multidimensional Bayesian analysis.[2] It is also encountered in wireless communications, while analyzing the performance of Rayleigh fading MIMO wireless channels .[3]
Probability density function
The Wishart distribution can be characterized by its probability density function as follows:
Let {{math|X}} be a {{math|p × p}} symmetric matrix of random variables that is positive definite. Let {{math|V}} be a (fixed) symmetric positive definite matrix of size {{math|p × p}}.
Then, if {{math|n ≥ p}}, {{math|X}} has a Wishart distribution with {{mvar|n}} degrees of freedom if it has the probability density function
where 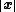 is the determinant of
is the determinant of  and {{math|Γp}} is the multivariate gamma function defined as
and {{math|Γp}} is the multivariate gamma function defined as
The density above is not the joint density of all the  elements of the random matrix {{math|X}} (such {{nowrap|
elements of the random matrix {{math|X}} (such {{nowrap| -dimensional}} density does not exists because of the symmetry constrains
-dimensional}} density does not exists because of the symmetry constrains 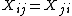 ), it is rather the joint density of
), it is rather the joint density of  elements
elements  for
for  ([1], page 38). Also, the density formula above applies only to positive definite matrices
([1], page 38). Also, the density formula above applies only to positive definite matrices 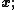 for other matrices the density is equal to zero.
for other matrices the density is equal to zero.
The joint-eigenvalue density for eigenvalues  is
is
where 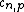 is a constant.
is a constant.
In fact the above definition can be extended to any real {{math|n > p − 1}}. If {{math|n ≤ p − 1}}, then the Wishart no longer has a density—instead it represents a singular distribution that takes values in a lower-dimension subspace of the space of {{math|p × p}} matrices.[4]
Use in Bayesian statistics
In Bayesian statistics, in the context of the multivariate normal distribution, the Wishart distribution is the conjugate prior to the precision matrix {{math|Ω {{=}} Σ−1}}, where {{math|Σ}} is the covariance matrix.[6]{{rp|135}}
Choice of parameters
The least informative, proper Wishart prior is obtained by setting {{math|n {{=}} p}}.{{Citation needed|date=June 2014}}
The prior mean of {{math|Wp(V, n)}} is {{math|nV}}, suggesting that a reasonable choice for {{math|V}} would be {{math|n−1Σ0}}, where {{math|Σ0}} is some prior guess for the covariance matrix.
Properties
Log-expectation
The following formula plays a role in variational Bayes derivations for Bayes networks
involving the Wishart distribution: [6]{{rp|693}}
where  is the multivariate digamma function (the derivative of the log of the multivariate gamma function).
is the multivariate digamma function (the derivative of the log of the multivariate gamma function).
Log-variance
The following variance computation could be of help in Bayesian statistics:
where 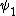 is the trigamma function. This comes up when computing the Fisher information of the Wishart random variable.
is the trigamma function. This comes up when computing the Fisher information of the Wishart random variable.
Entropy
The information entropy of the distribution has the following formula:[6]{{rp|693}}
where {{math|B(V, n)}} is the normalizing constant of the distribution:
This can be expanded as follows:
Cross-entropy
The cross entropy of two Wishart distributions  with parameters
with parameters 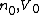 and
and  with parameters
with parameters 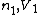 is
is
Note that when 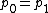 we recover the entropy.
we recover the entropy.
KL-divergence
The Kullback–Leibler divergence of  from
from  is
is
Characteristic function
The characteristic function of the Wishart distribution is
In other words,
where {{math|E[⋅]}} denotes expectation. (Here {{math|Θ}} and {{math|I}} are matrices the same size as {{math|V}}({{math|I}} is the identity matrix); and {{mvar|i}} is the square root of −1).[5]
Since the determinant's range contains a closed line through the origin for matrix dimensions greater than two, the above formula is only correct for small values of the Fourier variable. (see https://arxiv.org/pdf/1901.09347.pdf)
Theorem
If a {{math|p × p}} random matrix {{math|X}} has a Wishart distribution with {{mvar|m}} degrees of freedom and variance matrix {{math|V}} — write 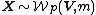 — and {{math|C}} is a {{math|q × p}} matrix of rank {{mvar|q}}, then [6]
— and {{math|C}} is a {{math|q × p}} matrix of rank {{mvar|q}}, then [6]
Corollary 1
If {{math|z}} is a nonzero {{math|p × 1}} constant vector, then:[6]
In this case, 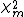 is the chi-squared distribution and
is the chi-squared distribution and 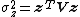 (note that
(note that  is a constant; it is positive because {{math|V}} is positive definite).
is a constant; it is positive because {{math|V}} is positive definite).
Corollary 2
Consider the case where {{math|zT {{=}} (0, ..., 0, 1, 0, ..., 0)}} (that is, the {{mvar|j}}-th element is one and all others zero). Then corollary 1 above shows that
gives the marginal distribution of each of the elements on the matrix's diagonal.
George Seber points out that the Wishart distribution is not called the “multivariate chi-squared distribution” because the marginal distribution of the off-diagonal elements is not chi-squared. Seber prefers to reserve the term multivariate for the case when all univariate marginals belong to the same family.[7]Estimator of the multivariate normal distribution
The Wishart distribution is the sampling distribution of the maximum-likelihood estimator (MLE) of the covariance matrix of a multivariate normal distribution.[8] A derivation of the MLE uses the spectral theorem.
Bartlett decomposition
The Bartlett decomposition of a matrix {{math|X}} from a {{mvar|p}}-variate Wishart distribution with scale matrix {{math|V}} and {{mvar|n}} degrees of freedom is the factorization:
where {{math|L}} is the Cholesky factor of {{math|V}}, and:
where 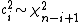 and {{math|nij ~ N(0, 1)}} independently.[9] This provides a useful method for obtaining random samples from a Wishart distribution.[10]
and {{math|nij ~ N(0, 1)}} independently.[9] This provides a useful method for obtaining random samples from a Wishart distribution.[10]
Marginal distribution of matrix elements
Let {{math|V}} be a {{math|2 × 2}} variance matrix characterized by correlation coefficient {{math|−1 < ρ < 1}} and {{math|L}} its lower Cholesky factor:
Multiplying through the Bartlett decomposition above, we find that a random sample from the {{math|2 × 2}} Wishart distribution is
The diagonal elements, most evidently in the first element, follow the {{math|χ2}} distribution with {{mvar|n}} degrees of freedom (scaled by {{math|σ2}}) as expected. The off-diagonal element is less familiar but can be identified as a normal variance-mean mixture where the mixing density is a {{math|χ2}} distribution. The corresponding marginal probability density for the off-diagonal element is therefore the variance-gamma distribution
where {{math|Kν(z)}} is the modified Bessel function of the second kind.[11] Similar results may be found for higher dimensions, but the interdependence of the off-diagonal correlations becomes increasingly complicated. It is also possible to write down the moment-generating function even in the noncentral case (essentially the nth power of Craig (1936)[12] equation 10) although the probability density becomes an infinite sum of Bessel functions.
The range of the shape parameter
It can be shown [13] that the Wishart distribution can be defined if and only if the shape parameter {{math|n}} belongs to the set
This set is named after Gindikin, who introduced it[14] in the seventies in the context of gamma distributions on homogeneous cones. However, for the new parameters in the discrete spectrum of the Gindikin ensemble, namely,
the corresponding Wishart distribution has no Lebesgue density.
Relationships to other distributions
- The Wishart distribution is related to the inverse-Wishart distribution, denoted by
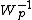 , as follows: If {{math|X ~ Wp(V, n)}} and if we do the change of variables {{math|C {{=}} X−1}}, then
, as follows: If {{math|X ~ Wp(V, n)}} and if we do the change of variables {{math|C {{=}} X−1}}, then  . This relationship may be derived by noting that the absolute value of the Jacobian determinant of this change of variables is {{math|{{!}}C{{!}}p+1}}, see for example equation (15.15) in.[15]
. This relationship may be derived by noting that the absolute value of the Jacobian determinant of this change of variables is {{math|{{!}}C{{!}}p+1}}, see for example equation (15.15) in.[15] - In Bayesian statistics, the Wishart distribution is a conjugate prior for the precision parameter of the multivariate normal distribution, when the mean parameter is known.[16]
- A generalization is the multivariate gamma distribution.
- A different type of generalization is the normal-Wishart distribution, essentially the product of a multivariate normal distribution with a Wishart distribution.
See also
{{Colbegin}}- Chi-squared distribution
- Complex Wishart distribution
- F-distribution
- Gamma distribution
- Hotelling's T-squared distribution
- Inverse-Wishart distribution
- Multivariate gamma distribution
- Student's t-distribution
- Wilks' lambda distribution
References
2. ^{{cite book |last=Gelman |first=Andrew |date=2003 |title=Bayesian Data Analysis |url=http://www.stat.columbia.edu/~gelman/book/ |publisher=Chapman & Hall |page=582 |isbn=158488388X |access-date=3 June 2015 |location=Boca Raton, Fla. |edition=2nd}}
3. ^{{cite journal| last=Zanella| first=A.|author2=Chiani, M. |author3=Win, M.Z. |title=On the marginal distribution of the eigenvalues of wishart matrices| journal=IEEE Transactions on Communications|date=April 2009| volume=57| issue=4| pages=1050–1060 | doi=10.1109/TCOMM.2009.04.070143}}
4. ^{{Cite journal | doi = 10.1214/aos/1176325375| title = On Singular Wishart and Singular Multivariate Beta Distributions| journal = The Annals of Statistics| volume = 22| pages = 395–405| year = 1994| last1 = Uhlig | first1 = H. }}
5. ^{{cite book | last = Anderson | first = T. W. | authorlink = T. W. Anderson | title = An Introduction to Multivariate Statistical Analysis | publisher = Wiley Interscience | edition = 3rd | location = Hoboken, N. J. | year = 2003 | page = 259 | isbn = 0-471-36091-0 }}
6. ^1 {{cite book |last=Rao |first=C. R. |title=Linear Statistical Inference and its Applications |location= |publisher=Wiley |year=1965 |page=535 }}
7. ^{{cite book | last = Seber | first = George A. F. | title = Multivariate Observations | publisher = Wiley | year = 2004 | isbn = 978-0471691211 }}
8. ^{{cite book |first=C. |last=Chatfield |first2=A. J. |last2=Collins |year=1980 |title=Introduction to Multivariate Analysis |location=London |publisher=Chapman and Hall |pages=103–108 |isbn=0-412-16030-7 }}
9. ^{{cite book | last = Anderson | first = T. W. | authorlink = T. W. Anderson | title = An Introduction to Multivariate Statistical Analysis | publisher = Wiley Interscience | edition = 3rd | location = Hoboken, N. J. | year = 2003 | page = 257 | isbn = 0-471-36091-0 }}
10. ^{{cite journal |title=Algorithm AS 53: Wishart Variate Generator |first1= W. B. |last1=Smith |first2= R. R. |last2=Hocking |journal=Journal of the Royal Statistical Society, Series C |volume=21 |issue=3 |year=1972 |pages=341–345 |jstor=2346290}}
11. ^{{cite journal | last1 = Pearson | first1 = Karl | author1-link = Karl Pearson | last2 = Jeffery | first2 = G. B. | author2-link = George Barker Jeffery | last3 = Elderton | first3 = Ethel M. | author3-link = Ethel M. Elderton | title = On the Distribution of the First Product Moment-Coefficient, in Samples Drawn from an Indefinitely Large Normal Population | journal = Biometrika | volume = 21 | issue = | pages = 164–201 | publisher = Biometrika Trust | date = December 1929 | jstor = 2332556 | doi = 10.2307/2332556}}
12. ^{{cite journal | last = Craig | first = Cecil C. | title = On the Frequency Function of xy | journal = Ann. Math. Statist. | volume = 7 | issue = | pages = 1–15 | year = 1936 | url = http://projecteuclid.org/euclid.aoms/1177732541 | doi = 10.1214/aoms/1177732541}}
13. ^{{cite journal |doi=10.1214/aop/1176990455 |last=Peddada and Richards |first1=Shyamal Das |last2=Richards |first2=Donald St. P. |title=Proof of a Conjecture of M. L. Eaton on the Characteristic Function of the Wishart Distribution, |journal=Annals of Probability |volume=19 |issue=2 |pages=868–874 |year=1991 }}
14. ^{{cite journal |doi=10.1007/BF01078179 |first=S.G. |last=Gindikin |title=Invariant generalized functions in homogeneous domains, |journal=Funct. Anal. Appl. |volume=9 |issue=1 |pages=50–52 |year=1975}}
15. ^{{cite journal |first=Paul S. |last=Dwyer |title=Some Applications of Matrix Derivatives in Multivariate Analysis |journal=J. Amer. Statist. Assoc. |year=1967 |volume=62 |issue=318 |pages=607–625 |jstor=2283988 }}
16. ^1 2 3 {{cite book |first=C. M. |last=Bishop |title=Pattern Recognition and Machine Learning |location= |publisher=Springer |year=2006 }}
External links
- [https://github.com/zweng/rmg A C++ library for random matrix generator]
- 1960-61 American Hockey League season
- 1960-61 Indian cricket season
- 1960-61 National Basketball Association season
- 1960-61 National Hockey League season
- 1960-61 New Zealand cricket season
- 1960-61 nhl season
- 1960-61 Pakistani cricket season
- 1960-61 South African cricket season
- 1960-61 West Indian cricket season
- 1960 Academy Awards
- 1960 AFL season
- 1960 Agadir earthquake
- 1960 All-AFL Team
- 1960 American Football League Championship Game
- 1960 American Football League season
- 1960 Armstrong 500
- 1960 Australasian Championships
- 1960 Australian Championships
- 1960 Australian Championships – Men's Singles
- 1960 Australian Championships – Women's Singles
- 1960 Australian Touring Car Championship
- 1960 Baltimore Orioles season
- 1960 Belgian Congo general election
- 1960 Boston Patriots season
- 1960 Boston Red Sox season