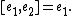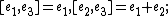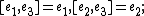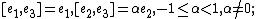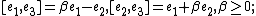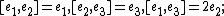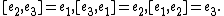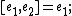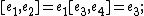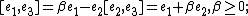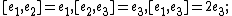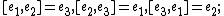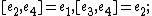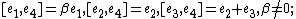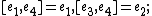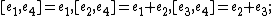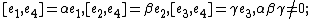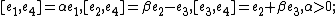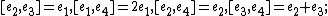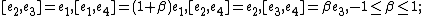- One-dimensional Two-dimensional Three-dimensional Four-dimensional
- Notes
In mathematics, there is a classification of low-dimensional real Lie algebras.
Let 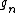 be
be  -dimensional Lie algebra over the field of real numbers
-dimensional Lie algebra over the field of real numbers
with generators 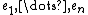 ,
, 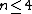 .{{clarify|Here and the in the below, I’m not completely sure how the notations work|date=December 2018}} Below we give Mubarakzyanov's classification[1] and numeration of these algebras. For review see also Popovych et al.[2] For each algebra
.{{clarify|Here and the in the below, I’m not completely sure how the notations work|date=December 2018}} Below we give Mubarakzyanov's classification[1] and numeration of these algebras. For review see also Popovych et al.[2] For each algebra 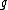 we adduce only non-zero commutators between basis elements.
we adduce only non-zero commutators between basis elements.
One-dimensional
-
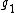 , abelian.
, abelian.
Two-dimensional
-
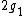 , abelian;
, abelian; -
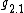 , solvable,
, solvable,
Three-dimensional
-
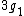 , abelian, Bianchi I;
, abelian, Bianchi I; -
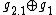 , decomposable solvable, Bianchi III;
, decomposable solvable, Bianchi III; -
 , Heisenberg–Weyl algebra, nilpotent, Bianchi II,
, Heisenberg–Weyl algebra, nilpotent, Bianchi II,
-
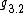 , solvable, Bianchi IV,
, solvable, Bianchi IV,
-
 , solvable, Bianchi V,
, solvable, Bianchi V,
-
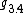 , solvable, Bianchi VI, Poincaré algebra
, solvable, Bianchi VI, Poincaré algebra 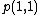 when
when 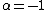 ,
,
-
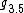 , solvable, Bianchi VII,
, solvable, Bianchi VII,
-
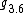 , simple, Bianchi VIII,
, simple, Bianchi VIII, 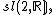
-
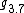 , simple, Bianchi VIII,
, simple, Bianchi VIII, 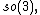
Algebra  can be considered as an extreme case of
can be considered as an extreme case of 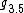 , when
, when 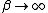 , forming contraction of Lie algebra.
, forming contraction of Lie algebra.
Over the field  algebras
algebras 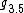 ,
, 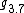 are isomorphic to
are isomorphic to 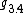 and
and 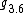 , respectively.
, respectively.
Four-dimensional
-
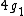 , abelian;
, abelian; -
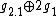 , decomposable solvable,
, decomposable solvable,
-
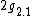 , decomposable solvable,
, decomposable solvable,
-
 , decomposable nilpotent,
, decomposable nilpotent,
-
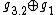 , decomposable solvable,
, decomposable solvable,
-
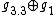 , decomposable solvable,
, decomposable solvable,
-
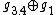 , decomposable solvable,
, decomposable solvable,
-
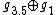 , decomposable solvable,
, decomposable solvable,
-
 , unsolvable,
, unsolvable,
-
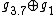 , unsolvable,
, unsolvable,
-
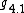 , indecomposable nilpotent,
, indecomposable nilpotent,
-
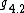 , indecomposable solvable,
, indecomposable solvable,
-
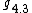 , indecomposable solvable,
, indecomposable solvable,
-
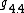 , indecomposable solvable,
, indecomposable solvable,
-
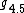 , indecomposable solvable,
, indecomposable solvable,
-
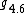 , indecomposable solvable,
, indecomposable solvable,
-
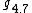 , indecomposable solvable,
, indecomposable solvable,
-
 , indecomposable solvable,
, indecomposable solvable,
-
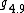 , indecomposable solvable,
, indecomposable solvable,
-
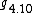 , indecomposable solvable,
, indecomposable solvable,
Algebra 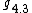 can be considered as an extreme case of
can be considered as an extreme case of 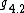 , when
, when 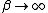 , forming contraction of Lie algebra.
, forming contraction of Lie algebra.
Over the field  algebras
algebras 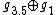 ,
, 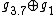 ,
, 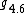 ,
, 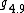 ,
, 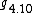 are isomorphic to
are isomorphic to 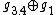 ,
,  ,
, 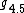 ,
,  ,
, 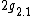 , respectively.
, respectively.
Notes
2. ^{{harvnb|Popovych|2003}}
- Alcanhões
- Alcan International
- Alcanivoracaceae
- Alcanivoraceae
- Alcanivorax borkumensis
- Alcaniz
- Alcaniz CF
- Alcanizo
- Alcanizo, Spain
- Alcanizo, Toledo
- Alcanna tinctoria
- Al Cannava
- Alcano
- Alcanol
- Alcanon
- Alcant
- Alcantara accident
- Alcantara Bridge
- Alcantara (disambiguation)
- Alcantara (Lisbon)
- Alcantara, Lisbon
- Alcantara Machado
- Alcantara, Maranhao
- Alcantara, Maranhão
- Alcantara, Military Order of