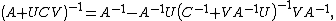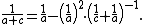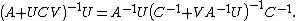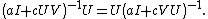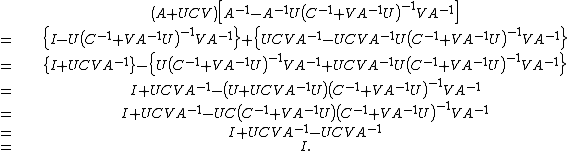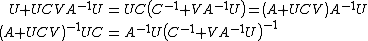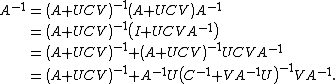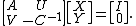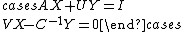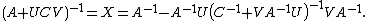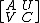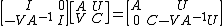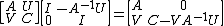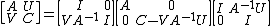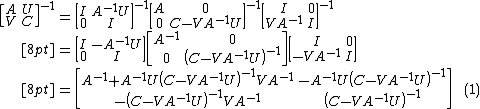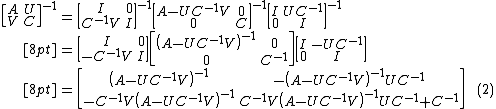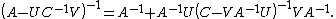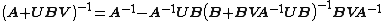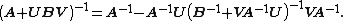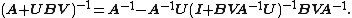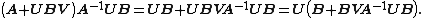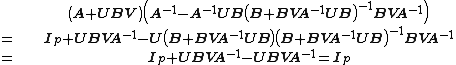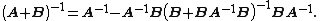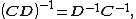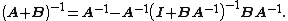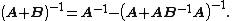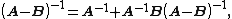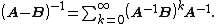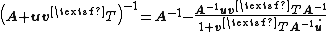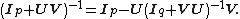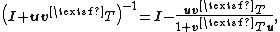“Woodbury matrix identity”的意思、由来-开放百科全书

In mathematics (specifically linear algebra), the Woodbury matrix identity, named after Max A. Woodbury^[1]^[2] says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix. Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the Woodbury report.^[3]

where A, U, C and V all denote matrices of the correct (conformable) sizes. Specifically, A is n-by-n, U is n-by-k, C is k-by-k and V is k-by-n. This can be derived using blockwise matrix inversion.

For a more general formula for which the matrix C need not be invertible or even square, see Binomial inverse theorem.

Special cases

When C is the 1-by-1 unit matrix, this identity reduces to the Sherman–Morrison formula. In the case when C is the identity matrix I, the matrix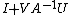

is known in numerical linear algebra and numerical partial differential equations as the capacitance matrix.^[3] For mere numbers, the identity reduces to the following relation of fractions

Push-through identity

Multiplying on the right by

and simplifying yields the following push-through identity^[6]

The special case where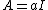

and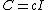

(where these two identity matrices have different sizes in general) illustrates the origin of the "push-through" name:

Direct proof

The formula can be proven by checking that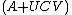

times its alleged inverse on the right side of the Woodbury identity gives the identity matrix:

Algebraic proof

Derivation via blockwise elimination

Deriving the Woodbury matrix identity is easily done by solving the following block matrix inversion problem

which is equivalent to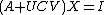

. Eliminating the first equation, we find that

, which can be substituted into the second to find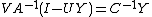

. Expanding and rearranging, we have

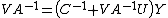, or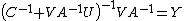

. Finally, we substitute into our

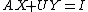, and we have

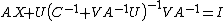. Thus,

Derivation from LDU decomposition

which is the LDU decomposition of the block matrix into an upper triangular, diagonal, and lower triangular matrices.

We could equally well have done it the other way (provided that C is invertible) i.e.

Now comparing elements (1, 1) of the RHS of (1) and (2) above gives the Woodbury formula

Applications

This identity is useful in certain numerical computations where A⁻¹ has already been computed and it is desired to compute (A + UCV)⁻¹. With the inverse of A available, it is only necessary to find the inverse of C⁻¹ + VA⁻¹U in order to obtain the result using the right-hand side of the identity. If C has a much smaller dimension than A, this is more efficient than inverting A + UCV directly. A common case is finding the inverse of a low-rank update A + UCV of A (where U only has a few columns and V only a few rows), or finding an approximation of the inverse of the matrix A + B where the matrix B can be approximated by a low-rank matrix UCV, for example using the singular value decomposition.

This is applied, e.g., in the Kalman filter and recursive least squares methods, to replace the parametric solution, requiring inversion of a state vector sized matrix, with a condition equations based solution. In case of the Kalman filter this matrix has the dimensions of the vector of observations, i.e., as small as 1 in case only one new observation is processed at a time. This significantly speeds up the often real time calculations of the filter.

Binomial inverse theorem

The binomial inverse theorem is a more general form of the Woodbury matrix identity.

provided A and B + BVA⁻¹UB are nonsingular. Nonsingularity of the latter requires that B⁻¹ exist since it equals {{nowrap|B(I + VA⁻¹UB)}} and the rank of the latter cannot exceed the rank of B.^[5]

Since B is invertible, the two B terms flanking the parenthetical quantity inverse in the right-hand side can be replaced with {{nowrap|(B⁻¹)⁻¹,}} which results in

This is the Woodbury matrix identity, which can also be derived using matrix blockwise inversion.

A more general formula exists when B is singular and possibly even non-square:^[5]

Verification

So we get that if A⁻¹ and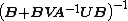

exist, then

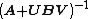exists and is given by the theorem above.^[7]

Special cases

First

Continuing with the merging of the terms of the far right-hand side of the above equation results in Hua's identity

This form can be used in perturbative expansions where B is a perturbation of A.

Second

If B = I_q is the identity matrix and q = 1, then U is a column vector, written u, and V is a row vector, written v^T. Then the theorem implies the Sherman-Morrison formula:

This is useful if one has a matrix A with a known inverse A⁻¹ and one needs to invert matrices of the form A + uv^T quickly for various u and v.

Third

See also

Notes

1. ^Max A. Woodbury, Inverting modified matrices, Memorandum Rept. 42, Statistical Research Group, Princeton University, Princeton, NJ, 1950, 4pp {{MR|38136}}
2. ^Max A. Woodbury, The Stability of Out-Input Matrices. Chicago, Ill., 1949. 5 pp. {{MR|32564}}
3. ^¹{{cite journal |first=William W. |last=Hager |title=Updating the inverse of a matrix |journal=SIAM Review |volume=31 |year=1989 |pages=221–239 |issue=2 |doi=10.1137/1031049 |mr=997457 | jstor = 2030425}}
4. ^{{Cite book | last1=Higham | first1=Nicholas | author1-link=Nicholas Higham | title=Accuracy and Stability of Numerical Algorithms | publisher=SIAM | edition=2nd | isbn=978-0-89871-521-7 | year=2002 | page=258 |mr=1927606 | postscript= }}
5. ^¹²{{cite journal | last1 = Henderson | first1 = H. V. | last2 = Searle | first2 = S. R. | year = 1981 | title = On deriving the inverse of a sum of matrices | url = http://ecommons.cornell.edu/bitstream/1813/32749/1/BU-647-M.pdf| journal = SIAM Review | volume = 23 | issue = | pages = 53–60 | doi = 10.1137/1023004 | jstor = 2029838 }}
6. ^Kurt S. Riedel, "A Sherman–Morrison–Woodbury Identity for Rank Augmenting Matrices with Application to Centering", SIAM Journal on Matrix Analysis and Applications, 13 (1992)659-662, {{doi|10.1137/0613040}} preprint {{MR|1152773}}
7. ^{{cite book | author = Gilbert Strang | title = Introduction to Linear Algebra | edition = 3rd | year = 2003 | publisher = Wellesley-Cambridge Press: Wellesley, MA | isbn = 0-9614088-9-8}}

Special cases

Push-through identity

Direct proof

Algebraic proof

Derivation via blockwise elimination

Derivation from LDU decomposition

Applications

Binomial inverse theorem

Verification

Special cases

First

Second

Third

See also

Notes

External links