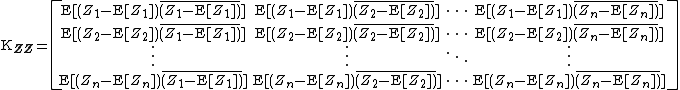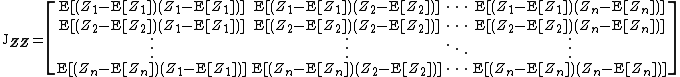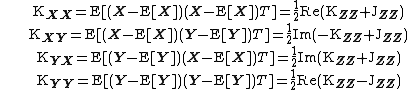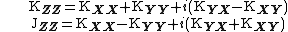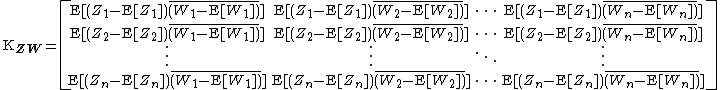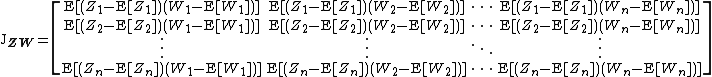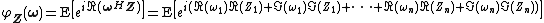- Definition
- Cumulative distribution function
- Expectation
- Covariance matrix and pseudo-covariance matrix Definitions Properties Covariance matrices of real and imaginary parts
- Cross-covariance matrix and pseudo-cross-covariance matrix Definitions Uncorrelatedness
- Independence
- Circular symmetry Definition Properties
- Proper complex random vectors Definition Properties
- Cauchy-Schwarz inequality
- Characteristic function
- See also
- References
In probability theory and statistics, a complex random vector is typically a tuple of complex-valued random variables, and generally is a random variable taking values in a vector space over the field of complex numbers. If 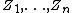 are complex-valued random variables, then the n-tuple
are complex-valued random variables, then the n-tuple 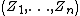 is a complex random vector. Complex random variables can always be considered as pairs of real random vectors: their real and imaginary parts.
is a complex random vector. Complex random variables can always be considered as pairs of real random vectors: their real and imaginary parts.
Some concepts of real random vectors have a straightforward generalization to complex random vectors. For example, the definition of the mean of a complex random vector. Other concepts are unique to complex random vectors.
Applications of complex random vectors are found in digital signal processing.
{{Probability fundamentals}}Definition
A complex random vector 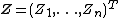 on the probability space
on the probability space 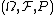 is a function
is a function  such that the vector
such that the vector 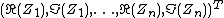 is a real real random vector on
is a real real random vector on 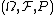 where
where 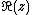 denotes the real part of
denotes the real part of  and
and 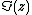 denotes the imaginary part of
denotes the imaginary part of  .[1]{{rp|p. 292}}
.[1]{{rp|p. 292}}
Cumulative distribution function
The generalization of the cumulative distribution function from real to complex random variables is not obvious because expressions of the form 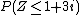 make no sense. However expessions of the form
make no sense. However expessions of the form 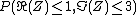 make sense. Therefore, the cumulative distribution function
make sense. Therefore, the cumulative distribution function 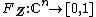 of a random vector
of a random vector 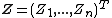 is defined as
is defined as
|indent =
|title=
|equation = {{NumBlk||
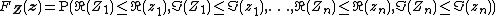 |{{EquationRef|Eq.1}}}}
|{{EquationRef|Eq.1}}}}|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where 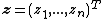 .
.
Expectation
As in the real case the expectation (also called expected value) of a complex random vector is taken component-wise.[1]{{rp|p. 293}}
{{Equation box 1|indent =
|title=
|equation = {{NumBlk||
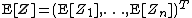 |{{EquationRef|Eq.2}}}}
|{{EquationRef|Eq.2}}}}|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
Covariance matrix and pseudo-covariance matrix
Definitions
The covariance matrix (also called second central moment) 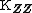 contains the covariances between all pairs of components. The covariance matrix of an
contains the covariances between all pairs of components. The covariance matrix of an  random vector is an
random vector is an  matrix whose
matrix whose  th element is the covariance between the i th and the j th random variables.[2]{{rp|p.372}} Unlike in the case of real random variables, the covariance between two random variables involves the complex conjugate of one of the two. Thus the covariance matrix is a Hermitian matrix.[1]{{rp|p. 293}}
th element is the covariance between the i th and the j th random variables.[2]{{rp|p.372}} Unlike in the case of real random variables, the covariance between two random variables involves the complex conjugate of one of the two. Thus the covariance matrix is a Hermitian matrix.[1]{{rp|p. 293}}
|indent =
|title=
|equation = {{NumBlk||
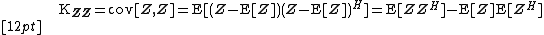
|{{EquationRef|Eq.3}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
The pseudo-covariance matrix (also called relation matrix) is defined as follows. In contrast to the covariance matrix defined above Hermitian transposition gets replaced by transposition in the definition.
{{Equation box 1|indent =
|title=
|equation = {{NumBlk||
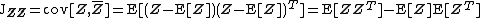
|{{EquationRef|Eq.4}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
Properties
The covariance matrix is a hermitian matrix, i.e.[1]{{rp|p. 293}}
.
The pseudo-covariance matrix is a symmetric matrix, i.e.
.
The covariance matrix is a positive semidefinite matrix, i.e.
.
Covariance matrices of real and imaginary parts
By decomposing the random vector  into its real part
into its real part 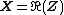 and imaginary part
and imaginary part 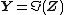 (i.e.
(i.e. 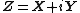 ), the matrices
), the matrices 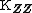 and
and 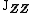 can be related to the covariance matrices of
can be related to the covariance matrices of  and
and 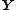 via the following expressions:
via the following expressions:
and conversely
Cross-covariance matrix and pseudo-cross-covariance matrix
Definitions
The cross-covariance matrix between two complex random vectors 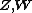 is defined as:
is defined as:
|indent =
|title=
|equation = {{NumBlk||
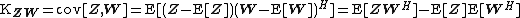 |{{EquationRef|Eq.5}}}}
|{{EquationRef|Eq.5}}}}|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
And the pseudo-cross-covariance matrix is defined as:
{{Equation box 1|indent =
|title=
|equation = {{NumBlk||
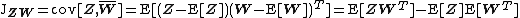 |{{EquationRef|Eq.6}}}}
|{{EquationRef|Eq.6}}}}|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
Uncorrelatedness
Two complex random vectors  and
and  are called uncorrelated if
are called uncorrelated if
.
Independence
{{main|Independence (probability theory)}}Two complex random vectors 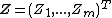 and
and 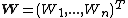 are called independent if
are called independent if
|indent =
|title=
|equation = {{NumBlk||
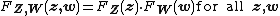 |{{EquationRef|Eq.7}}}}
|{{EquationRef|Eq.7}}}}|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where 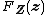 and
and 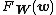 denote the cumulative distribution functions of
denote the cumulative distribution functions of  and
and  as defined in {{EquationNote|Eq.1}} and
as defined in {{EquationNote|Eq.1}} and  denotes their joint cumulative distribution function. Independence of
denotes their joint cumulative distribution function. Independence of  and
and  is often denoted by
is often denoted by 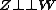 .
.
Written component-wise,  and
and  are called independent if
are called independent if
.
Circular symmetry
Definition
A complex random vector  is called circularly symmetric if for every deterministic
is called circularly symmetric if for every deterministic 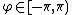 the distribution of
the distribution of 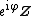 equals the distribution of
equals the distribution of  .[3]{{rp|pp. 500–501}}
.[3]{{rp|pp. 500–501}}
Properties
- The expectation of a circularly symmetric complex random vectors is either zero or it is not defined.[3]{{rp|p. 500}}
- The pseudo-covariance matrix of a circularly symmetric complex random vectors is zero.[3]{{rp|p. 584}}
Proper complex random vectors
Definition
A complex random vector  is called proper if the following three conditions are all satisfied:[1]{{rp|p. 293}}
is called proper if the following three conditions are all satisfied:[1]{{rp|p. 293}}
-
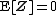 (zero mean)
(zero mean) -
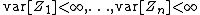 (all components have finite variance)
(all components have finite variance) -

Two complex random vectors 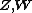 are called jointly proper is the composite random vector
are called jointly proper is the composite random vector 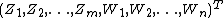 is proper.
is proper.
Properties
- A complex random vector
 is proper if, and only if, for all (deterministic) vectors
is proper if, and only if, for all (deterministic) vectors 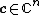 the complex random variable
the complex random variable 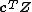 is proper.[1]{{rp|p. 293}}
is proper.[1]{{rp|p. 293}} - Linear transformations of proper complex random vectors are proper, i.e. if
 is a proper random vectors with
is a proper random vectors with  components and
components and  is a deterministic
is a deterministic  matrix, then the complex random vector
matrix, then the complex random vector 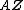 is also proper.[1]{{rp|p. 295}}
is also proper.[1]{{rp|p. 295}} - Every circularly symmetric complex random vector with finite variance of all its components is proper.[1]{{rp|p. 295}}
- There are proper complex random vectors that are not circularly symmetric.[1]{{rp|p. 504}}
- A real random vector is proper if and only if it is constant.
- Two jointly proper complex random vectors are uncorrelated if and only if their covariace matrix is zero, i.e. if
 .
.
Cauchy-Schwarz inequality
The Cauchy-Schwarz inequality for complex random vectors is
.
Characteristic function
The characteristic function of a complex random vector  with
with  components is a function
components is a function 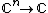 defined by:[1]{{rp|p. 295}}
defined by:[1]{{rp|p. 295}}
See also
- Complex random variable
References
2. ^{{cite book |first=John A. |last=Gubner |year=2006 |title=Probability and Random Processes for Electrical and Computer Engineers |publisher=Cambridge University Press |isbn=978-0-521-86470-1}}
3. ^1 2 {{cite book |first=David |last=Tse |year=2005 |title=Fundamentals of Wireless Communication |publisher=Cambridge University Press}}
- List of Duran Duran awards and nominations
- List of Durarara!! characters
- List of Durarara!! episodes
- List of Durarara episodes
- List of Durham County Cricket Club seasons
- List of Durham County episodes
- List of Dutch-Americans
- List of Dutch astronauts
- List of Dutch atheists
- List of Dutch Britons
- List of Dutch cabinets
- List of Dutch child actors
- List of Dutch classical composers
- List of Dutch comedians
- List of Dutch Comedians
- List of Dutch companies
- List of Dutch consorts
- List of Dutch East India Company trading posts
- List of Dutch family names
- List of Dutch films before 1910
- List of Dutch films of the 1920s
- List of Dutch films of the 1930s
- List of Dutch films of the 1940s
- List of Dutch films of the 1950s
- List of Dutch films of the 1960s