“Concavification”的意思、由来-开放百科全书

In mathematics, concavification is the process of converting a non-concave function to a concave function. A related concept is convexification – converting a non-convex function to a convex function. It is especially important in economics and mathematical optimization.^[1]

Concavification of a quasiconcave function by monotone transformation

An important special case of concavification is where the original function is a quasiconcave function. It is known that:

Therefore, a natural question is: given a quasiconcave function f(x), does there exist a monotonically increasing g(·) such that g(f(x)) is concave?

Positive and negative examples

As a positive example, consider the function

in the domain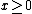

. This function is quasiconcave, but it is not concave (in fact, it is strictly convex). It can be concavified, for example, using the monotone transformation

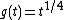, since

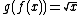which is concave.

A negative example was shown by Fenchel^[2]. His example is: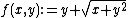

. He proved that this function is quasiconcave, but there is no monotone transformation g(·) such that g(f(x,y)) is concave.^[3]{{Rp|7–9}}

Based on these examples, we define a function to be concavifiable if there exists a monotone transformation that makes it concave. The question now becomes: what quasiconcave functions are concavifiable?

Concavifiability

Yakar Kannai treats the question in depth in the context of utility functions, giving sufficient conditions under which continuous convex preferences can be represented by concave utility functions.^[3]

His results were later generalized by Connell and Rasmussen,^[4] who give necessary and sufficient conditions for concavifiability. They show an example of a function that violates their conditions and thus is not concavifiable. It is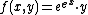

. They prove that this function is strictly quasiconcave and its gradient is non-vanishing, but it is not concavifiable.

References

1. ^{{Cite journal|last=Li|first=D.|last2=Sun|first2=X. L.|last3=Biswal|first3=M. P.|last4=Gao|first4=F.|date=2001-07-01|title=Convexification, Concavification and Monotonization in Global Optimization|journal=Annals of Operations Research|language=en|volume=105|issue=1–4|pages=213–226|doi=10.1023/A:1013313901854|issn=0254-5330}}
2. ^{{Cite book|url=|title=Convex cones, sets and functions|last=Fenchel|publisher=Princeton University|year=1953|isbn=|location=|pages=}}
3. ^{{Cite journal|date=1977-03-01|title=Concavifiability and constructions of concave utility functions|url=https://www.sciencedirect.com/science/article/pii/0304406877900155|journal=Journal of Mathematical Economics|language=en|volume=4|issue=1|pages=1–56|doi=10.1016/0304-4068(77)90015-5|issn=0304-4068|last1=Kannai|first1=Yakar}}
4. ^¹{{Cite journal|last=Connell|first=Christopher|last2=Rasmusen|first2=Eric Bennett|date=2012-08-17|title=Concavifying the QuasiConcave|url=https://papers.ssrn.com/abstract=1907180|language=en|location=Rochester, NY}}