“Contraction morphism”的意思、由来-开放百科全书

词条

Contraction morphism

释义

Birational perspective
See also
References

In algebraic geometry, a contraction morphism is a surjective projective morphism between normal projective varieties (or projective schemes) such that 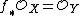or, equivalently, the geometric fibers are all connected (Zariski's connectedness theorem). It is also commonly called an algebraic fiber space, as it is an analog of a fiber space in algebraic topology.

By the Stein factorization, any surjective projective morphism is a contraction morphism followed by a finite morphism.

Examples include ruled surfaces and Mori fiber spaces.

Birational perspective

The following perspective is crucial in birational geometry (in particular in Mori's minimal model program).

Let X be a projective variety and 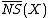the closure of the span of irreducible curves on X in 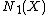= the real vector space of numerical equivalence classes of real 1-cycles on X. Given a face F of 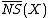, the contraction morphism associated to F, if it exists, is a contraction morphism to some projective variety Y such that for each irreducible curve , 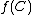is a point if and only if 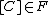.^[1] The basic question is which face F gives rise to such a contraction morphism (cf. cone theorem).

References

1. ^{{harvnb|Kollár–Mori|loc=Definition 1.25.}}

{{Citation | last1=Kollár | first1=János | last2=Mori | first2=Shigefumi | title=Birational geometry of algebraic varieties | publisher=Cambridge University Press | series=Cambridge Tracts in Mathematics | isbn=978-0-521-63277-5 |mr=1658959 | year=1998 | volume=134}}
Robert Lazarsfeld, Positivity in Algebraic Geometry I: Classical Setting (2004)

1 : Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Birational perspective

See also

References