“Delta-matroid”的意思、由来-开放百科全书

In mathematics, a delta-matroid or Δ-matroid is a family of sets obeying an exchange axiom generalizing an axiom of matroids. A non-empty family of sets is a delta-matroid if, for every two sets

and

in the family, and for every element

in their symmetric difference

, there exists an element

such that

. For the basis sets of a matroid, the corresponding exchange axiom requires in addition that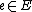

and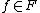

, ensuring that

and

have the same cardinality. For a delta-matroid, either of the two elements may belong to either of the two sets, and it is also allowed for the two elements to be equal.{{r|chun}}

An alternative an equivalent definition is that a family of sets forms a delta-matroid when the convex hull of its indicator vectors (the analogue of a matroid polytope) has the property that every edge length is either one or the square root of two.

Algorithms for matroid intersection and the matroid parity problem can be extended to some cases of delta-matroids.{{r|bj|gim}}

Delta-matroids have also been used to study constraint satisfaction problems.{{r|ff}} As a special case, an even delta-matroid is a delta-matroid in which all sets have an even number of elements. If a constraint satisfaction problem has a Boolean variable on each edge of a planar graph, and if the variables of the edges incident to each vertex of the graph are constrained to belong to an even delta-matroid (possibly a different even delta-matroid for each vertex), then the problem can be solved in polynomial time. This result plays a key role in a characterization of the planar Boolean constraint satisfaction problems that can be solved in polynomial time.{{r|kkr}}

References

1. ^{{citation | last = Bouchet | first = André | doi = 10.1007/BF02604639 | issue = 2 | journal = Mathematical Programming | mr = 904585 | pages = 147–159 | title = Greedy algorithm and symmetric matroids | volume = 38 | year = 1987}}
2. ^{{citation|url=http://matroidunion.org/?p=1882|title=Delta-matroids: Origins|date=July 13, 2016|first=Carolyn|last=Chun|work=The Matroid Union}}
3. ^{{citation | last1 = Feder | first1 = Tomás | last2 = Ford | first2 = Daniel | doi = 10.1137/S0895480104445009 | issue = 2 | journal = SIAM Journal on Discrete Mathematics | mr = 2257268 | pages = 372–394 | title = Classification of bipartite Boolean constraint satisfaction through delta-matroid intersection | volume = 20 | year = 2006}}
4. ^{{citation | last1 = Geelen | first1 = James F. | last2 = Iwata | first2 = Satoru | last3 = Murota | first3 = Kazuo | doi = 10.1016/S0095-8956(03)00039-X | issue = 2 | journal = Journal of Combinatorial Theory | mr = 1983366 | pages = 377–398 | series = Series B | title = The linear delta-matroid parity problem | volume = 88 | year = 2003}}
5. ^{{citation | last1 = Kazda | first1 = Alexandr | last2 = Kolmogorov | first2 = Vladimir | last3 = Rolínek | first3 = Michal | arxiv = 1602.03124 | date = December 2018 | doi = 10.1145/3230649 | issue = 2 | journal = ACM Transactions on Algorithms | pages = 22:1–22:33 | title = Even delta-matroids and the complexity of planar Boolean CSPs | volume = 15}}